(Temp save) |
|||
| Line 40: | Line 40: | ||
This makes sense. If a function is continuous then every point is exactly where we would "expect it to be". | This makes sense. If a function is continuous then every point is exactly where we would "expect it to be". | ||
[[Image:ContinuityGraph.jpg|450px|left|Graph Displaying Continuity]] | [[Image:ContinuityGraph.jpg|450px|left|Graph Displaying Continuity]] | ||
| + | |||
| + | As you can see by the graph, the green arrow shows a point on the graph that is exactly where we would expect it to be. The graph is continuous at this point. | ||
| + | |||
| + | The purple arrow shows a place where we would expect a point, but there isn't one there. The graph isn't continuous at that point. | ||
| + | |||
| + | The red arrow shows a point where we don't know what to expect. Coming from the left it looks like the graph should be the lower point. But coming from the right we would expect it to be the higher point. Since the function can't do both it isn't continuous at this point. This topic of approaching a limit from one direction or another brings us to our next topic. | ||
| + | |||
| + | ===Directional Limits=== | ||
| + | |||
| + | In the case of the graph above we may want to know the limit as we approach a point strictly from the left or from the right. We show this in our limit with a small plus or minus sign floating above the value. | ||
| + | |||
| + | For example. <math> \lim_{x\to 2^{-}}2x+1=5</math>. Notice that just because its <math>2^{-}</math> DOES NOT make it the same as <math>-2</math>. This means we take the limit as we approach the point 2 from numbers slightly less than 2. The same is true in reverse for <math>2^{+}</math> | ||
| + | |||
| + | ===Introducing Infinity=== | ||
| + | |||
| + | To set the record straight before we begin, infinity does not work like any other run of the mill number. It is, specifically by definition, not a number. A quick example of why not would be | ||
| + | <math>\infinity + 3=\infinity | ||
| + | |||
| + | \infinity - \infinity + 3 =\infinity - \infinity | ||
| + | |||
| + | 3=0</math> | ||
Revision as of 23:22, 31 October 2017
Work in Progress
Limits Approaching Infinity Intuitively
by Kevin LaMaster, proud Member of the Math Squad.
Contents
Introduction
I've noticed that many calculus one students loathe taking limits specifically as they approach infinity. This series should not be an introduction to limits nor should it replace a strict definition for a limit. Both of those can be found better at this tutorial. This only serves for a crash course tutor replacement for Calculus 1 students struggling with some difficult homework.
Basic Limits
Just as a recap over basic limits not into infinity.
Limits of Continuous functions
For the majority of limits the limit can just be found by plugging the values into the function.
For example $ \lim_{x\to 2}x^2+2x+1=2(2)^2+2(2)+1 $
The definition of a continuous function is that the limit at any point is equal to the value at that point.
The complicated math way to say this is $ \lim{x\to x_0}f(x)=f(x_0) $
This makes sense. If a function is continuous then every point is exactly where we would "expect it to be".
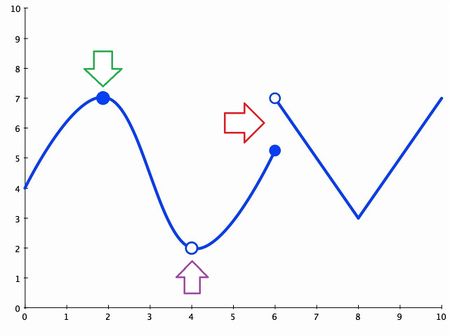
As you can see by the graph, the green arrow shows a point on the graph that is exactly where we would expect it to be. The graph is continuous at this point.
The purple arrow shows a place where we would expect a point, but there isn't one there. The graph isn't continuous at that point.
The red arrow shows a point where we don't know what to expect. Coming from the left it looks like the graph should be the lower point. But coming from the right we would expect it to be the higher point. Since the function can't do both it isn't continuous at this point. This topic of approaching a limit from one direction or another brings us to our next topic.
Directional Limits
In the case of the graph above we may want to know the limit as we approach a point strictly from the left or from the right. We show this in our limit with a small plus or minus sign floating above the value.
For example. $ \lim_{x\to 2^{-}}2x+1=5 $. Notice that just because its $ 2^{-} $ DOES NOT make it the same as $ -2 $. This means we take the limit as we approach the point 2 from numbers slightly less than 2. The same is true in reverse for $ 2^{+} $
Introducing Infinity
To set the record straight before we begin, infinity does not work like any other run of the mill number. It is, specifically by definition, not a number. A quick example of why not would be $ \infinity + 3=\infinity \infinity - \infinity + 3 =\infinity - \infinity 3=0 $