| Line 33: | Line 33: | ||
c) <math>\sim 9eV</math> | c) <math>\sim 9eV</math> | ||
| − | d) (2 | + | d) (2 1 0) |
<math>\rightarrow \:\frac{1}{2}\:\:\:\:1\:\:\:\:\infty </math> | <math>\rightarrow \:\frac{1}{2}\:\:\:\:1\:\:\:\:\infty </math> | ||
Latest revision as of 10:53, 6 August 2017
MICROELECTRONICS and NANOTECHNOLOGY (MN)
Question 2: Junction Devices
August 2011
Questions
All questions are in this link
Solutions of all questions
1) a) Direct bandgap semiconductors used in Lasers and LEDs. Photodetectors.
b) Si has a lattice matched $ SiO_2 $ to reduce surface defects. Si is almost 99\% pure.
c) $ \sim 9eV $
d) (2 1 0) $ \rightarrow \:\frac{1}{2}\:\:\:\:1\:\:\:\:\infty $
$ \rightarrow \:1\:\:\:\:2\:\:\:\:\infty $
e) $ \sim 900-1200 $ deg C.
------------------------------------------------------------------------------------
2) Neutral p $ \begin{align*} p_0&=10^{15}\\ n_0&=\frac{10^{20}}{10^{15}}=10^5 \end{align*} $ Neutral n $ \begin{align*} n_0&=10^{18}\\ p_0&=\frac{10^{20}}{10^{18}}=10^2 \end{align*} $
------------------------------------------------------------------------------------
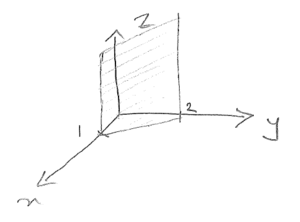
3)
$ \begin{align*} x_{n0}\cdot 10^{18}&=x_{p0}\cdot10^{15}\\ \implies x_{p0}&=10^3\times0.001\mu m = 1\mu m \end{align*} $
------------------------------------------------------------------------------------
4) $ x_n = \sqrt{\frac{2\epsilon}{q}\frac{N_A}{N_D(N_A+N_D)}\cdot(V_{bi}+V)} $
------------------------------------------------------------------------------------
5) $ \begin{align*} \rho &=\frac{1}{q\mu_nN_D} = \frac{1}{2\times10^{-19}\times500\times10^{18}}\\ &=\frac{1}{1000\times10^{-1}}\Omega\cdot cm\\ &=10^{-2}\Omega\cdot cm \end{align*} $ $ R_s=\frac{\rho}{L} =\frac{10^{-2}}{5\times10^{-4}} = 20\Omega/\Box $
------------------------------------------------------------------------------------ 6) $ \begin{align*} J_n&=q_n\mu_nE\\ &=2\times10^{-19}\times10^{18}\times500\times1000\\ &=10^5 A/cm^2 \end{align*} $ ------------------------------------------------------------------------------------ 7) $ \begin{align*} J_{diff} &=qD_n\frac{d\triangle n}{dx}\\ &=2\times10^{-19}\times500\times 25m\times\frac{\triangle n_p}{5\mu m}\\ \end{align*} $ ------------------------------------------------------------------------------------ 8)------------------------------------------------------------------------------------ 9)
------------------------------------------------------------------------------------ 10) Forward Active Mode
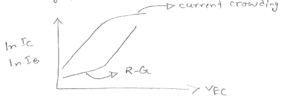
------------------------------------------------------------------------------------ 11)Fig 11.15(SDF) Page 425
$ \beta $ is reduced by both phenomena.
------------------------------------------------------------------------------------ 12)