| Line 32: | Line 32: | ||
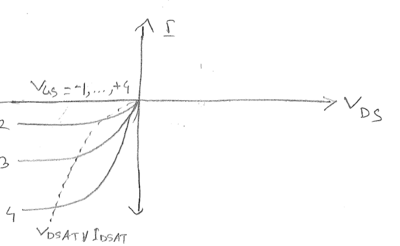
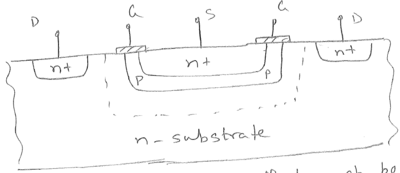
So consider p-channel MOSFET. | So consider p-channel MOSFET. | ||
| − | [[Image:MN3_09_1.png]] | + | [[Image:MN3_09_1.png| Alt text|400x400px]] |
<math>=\mu_pC_{ox}\frac{W}{L} = \mu_p\frac{\epsilon_{ox}}{t_{ox}}\frac{W}{L}</math> | <math>=\mu_pC_{ox}\frac{W}{L} = \mu_p\frac{\epsilon_{ox}}{t_{ox}}\frac{W}{L}</math> | ||
Latest revision as of 10:49, 6 August 2017
MICROELECTRONICS and NANOTECHNOLOGY (MN)
Question 3: Field Effect Devices
August 2009
Questions
All questions are in this link
Solutions of all questions
a) Previous year question.\\ b) $ V_T = -1V $ So consider p-channel MOSFET.
$ =\mu_pC_{ox}\frac{W}{L} = \mu_p\frac{\epsilon_{ox}}{t_{ox}}\frac{W}{L} $
$ \begin{align*} & t_{ox} \uparrow k\downarrow\\ & \mu_p \uparrow k\uparrow\\ & L \uparrow k\downarrow\\ & W \uparrow k\uparrow\\ & N_A \uparrow \text{ No change} \end{align*} $
$ V_{TH} = \psi_s+\frac{k_s}{k_{ox}}x_0\sqrt{\frac{2qN_A}{k_s\epsilon_0}\psi_s} $
chk only 2
f) square law $ \[Q_i=C_{ox}(V_{GS} - V_{th}-V)\] $
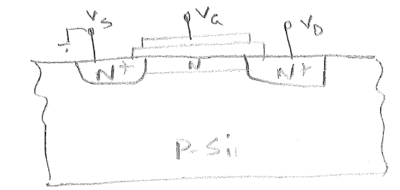
n-channel
Bulk charge
$ Q_i = -C_{ox}(V_{GS} - V_{th}-V))+\underbrace{qN_A[w_T(V)-w_T(V=0)]}_{\text{variation of $w_T$ with $V$ is considered}} $
------------------------------------------------------------------------------------
3)i)
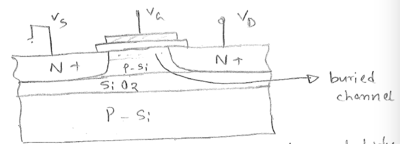
Turned on without any applied gate voltage.
Better control on channel due to lowered body effect.
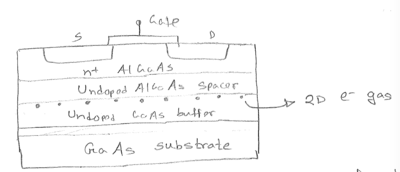
Very high speed device due to $e^-$ gas formation.
Can handle short channel effect much better
------------------------------------------------------------------------------------