| Line 28: | Line 28: | ||
===Solution 1=== | ===Solution 1=== | ||
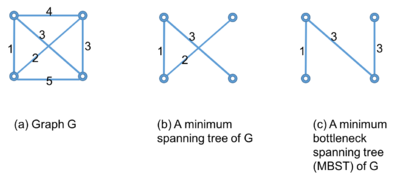
A MBST tree is not a minimum spanning tree for <math>G</math>, ABST may not contain the lightest edge. A counter example is showing in figure below: | A MBST tree is not a minimum spanning tree for <math>G</math>, ABST may not contain the lightest edge. A counter example is showing in figure below: | ||
| − | [[File:Q3-MBST-example.png| | + | [[File:Q3-MBST-example.png|400px]] |
[[ECE-QE_CE1-2013|Back to QE CE question 1, August 2013]] | [[ECE-QE_CE1-2013|Back to QE CE question 1, August 2013]] | ||
[[ECE_PhD_Qualifying_Exams|Back to ECE Qualifying Exams (QE) page]] | [[ECE_PhD_Qualifying_Exams|Back to ECE Qualifying Exams (QE) page]] | ||
Revision as of 18:32, 20 July 2017
Computer Engineering(CE)
Question 1: Algorithms
August 2013
Solution 1
A MBST tree is not always a MST.
Proof: Suppose we have a spanning tree $ T $ which is a MBST of $ G $ , and $ T $ is also a MST. The bottle neck is edge $ e $ with weight $ w $. Then I have another vertex $ X $ that will be connected to the graph $ G $ to form a new graphs $ G' $. $ \mathbf{G'} = \mathbf{G} +X $. And the possible edges that connect graph \mathbf{G} and new vertex $ X $ has weights $ w_1, w_2, ... W_x $, and each is no greater than the bottle neck weight $ w $. Using any of the edges from $ w_1, w_2, ... W_x $, I get a new tree $ T' $. S $ T' $ is still a spanning tree, and its largest weight remains $ w $, so $ T' $ is also an MBST. However, among these edges that I can choose to span the tree, only the one that has the smallest weight will be a MST, by definition. So an MBST for a graph $ G' $ is not a minimum spanning tree for $ \mathbf{G'} $. End of proof.
Solution 1
A MBST tree is not a minimum spanning tree for $ G $, ABST may not contain the lightest edge. A counter example is showing in figure below: