| Line 15: | Line 15: | ||
\end{cases}</math> | \end{cases}</math> | ||
| − | [[Image:A1FO32007.png|Alt text| | + | [[Image:A1FO32007.png|Alt text|328x342px]] |
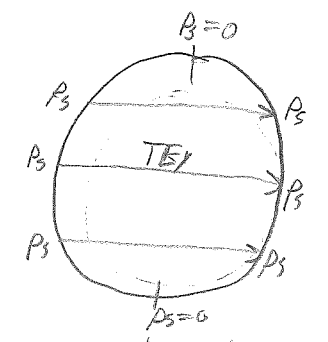
Consider case for <math>TE_x</math>; here the surface charge must match the normal component of <math>\bar{D}</math>. At the left and right sides of the circle, <math>\rho_s</math> goes to zero. This cannot happen in a PEC which must maintain a uniform potential. | Consider case for <math>TE_x</math>; here the surface charge must match the normal component of <math>\bar{D}</math>. At the left and right sides of the circle, <math>\rho_s</math> goes to zero. This cannot happen in a PEC which must maintain a uniform potential. | ||
Latest revision as of 10:33, 18 June 2017
1-a) No, these modes cannot be supported
$ E_{1t}\ne E_{2t =0} $
------------------------------------------------------------------------------------
b)
\underline{BC's}
$ \begin{cases} E_{1t}= E_{2t} =0\\ D_{1n} = \rho_s\\ H_{1t} = J_s\\ B_{1n}= B_{2n} =0 \end{cases} $
Consider case for $ TE_x $; here the surface charge must match the normal component of $ \bar{D} $. At the left and right sides of the circle, $ \rho_s $ goes to zero. This cannot happen in a PEC which must maintain a uniform potential.
------------------------------------------------------------------------------------ 2) $ TM_z (H_z =0) $ ------------------------------------------------------------------------------------ a) Yes, it can support $ TM{_z} $ waves. ------------------------------------------------------------------------------------ b This is effectively a rectangular waveguide (which can support $ TM_z $) an additional boundary condition at $ x=d $. At this boundary, only $ \bar{E} $ is effected: $ \begin{cases} E_{1t}= E_{2t} \\ D_{1n} = D_{2n}\to \epsilon_0E_{in} = \epsilon E_{2n}\\ H_{1t} = H_{2t}\\ H_{1n}= H_{2n} =0 \end{cases} $
(wrong?)
------------------------------------------------------------------------------------\\
$ \begin{cases} \nabla\times H_{1} = j\omega\epsilon_1 E_{1}\\ \nabla\times H_{2} = j\omega\epsilon_2 E_{2}\\ \end{cases} $
$ H_z =0 $
$ H_1 = (H_{1x}\hat{x}+H_{2y}\hat{y})e^{-jkz} $
$ H_2 = (\frac{\mu1}{\mu2}H_{1x}\hat{x}+H_{1y}\hat{y})e^{-jkz} $
$ \begin{cases} \to j\omega\epsilon_1 E_{1x} = jk_zH_{1y}\\ j\omega\epsilon_2 E_{2x} = jk_zH_{1y}\\ \end{cases} \epsilon_1E_{1x}=\epsilon_2E_{2x} $
$ \begin{cases} j\omega\epsilon_1 E_{1y} = jk_zH_{1x}\\ j\omega\epsilon_2 E_{2y} = jk_zH_{1x}\frac{\mu1}{\mu2}\\ \end{cases} E_{1y}=E_{2y}\to\frac{\epsilon_1}{\epsilon_2} = \frac{\mu_2}{\mu_1}\to \text{ can't exist} $
------------------------------------------------------------------------------------ 3) $ \nabla^2H_z + k^2H_z =0 $ $ \bar{H} = \bar{H}(x,y)e^{-kz} $ $ \frac{\partial^2H_z}{\partial x^2} + \frac{\partial^2H_z}{\partial y^2}+k^2H_z=0 $ \underline{BC's:PMC:} $ \begin{cases} H_z = 0\text{ at } x=0\\ H_z = 0\text{ at } x=a\\ H_z = 0\text{ at } y=0\\ H_z = 0\text{ at } y=b\\ \end{cases} $
$ H_z = H_0\sin\bigg(\frac{m\pi x}{a}\bigg)\sin\bigg(\frac{n\pi y}{b}\bigg)\cos(\omega t-kz) $