(Created page with "Category:ECE438Fall2016Boutin Category:ECE438 Category:ECE Category:fourier transform Category:homework =Homework 9 Solution, ECE438,...") |
|||
| Line 74: | Line 74: | ||
*Set <math>x[n]=\delta[n]</math> to get the unit impulse response h[n] of the system. Then Fourier transform $h[n]$ to get the frequency response. | *Set <math>x[n]=\delta[n]</math> to get the unit impulse response h[n] of the system. Then Fourier transform $h[n]$ to get the frequency response. | ||
*Set <math>x[n]=\delta[n]</math> to get the unit impulse response h[n] of the system. Then z-transform $h[n]$ to get the transfer function of the system, and subsequently restrict the transfer function to the unit circle to get the frequency response. | *Set <math>x[n]=\delta[n]</math> to get the unit impulse response h[n] of the system. Then z-transform $h[n]$ to get the transfer function of the system, and subsequently restrict the transfer function to the unit circle to get the frequency response. | ||
| − | *Take the Fourier transform of the left-hand-side and right-hand-side of the equation. Then use the fact that <math>\frac{{\mathcal Y}(\omega)}{{\mathcal Y}(\omega) | + | *Take the Fourier transform of the left-hand-side and right-hand-side of the equation. Then use the fact that <math>\frac{{\mathcal Y}(\omega)}{{\mathcal Y}(\omega)}={\mathcal H}(\omega)</math> to get the frequency response of the system. |
| − | *Take the z-transform of the left-hand-side and right-hand-side of the equation. Then use the fact that <math>\frac | + | *Take the z-transform of the left-hand-side and right-hand-side of the equation. Then use the fact that <math>\frac{Y(z)}{X(z)}=H(z)</math> to get the transfer function of the system. Finally restrict the transfer function to the unit circle to get the frequency response. |
---- | ---- | ||
Latest revision as of 13:33, 24 November 2016
Contents
Homework 9 Solution, ECE438, Fall 2016, Prof. Boutin
Question 1
a)
$ y[n]= \frac{x[n]+x[n-2]}{2} $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y[z]&= \frac{X[z]+X[z]z^{-2}}{2} \\ \frac{Y[z]}{X[z]}&= \frac{1+z^{-2}}{2} \\ H[z] &= \frac{1+z^{-2}}{2} \\ \end{align} $
Frequency Response $ H(\omega) $
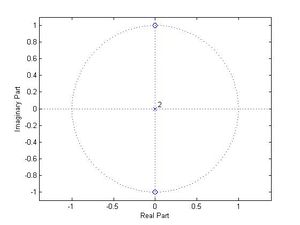
$ \begin{align} H[e^{j\omega }] &= \frac{1+e^{-2j\omega }}{2} \\ &= e^{-j\omega } \left( \frac{e^{j\omega}+e^{-j\omega}}{2} \right) \\ &= e^{-j\omega } cos \left( \omega \right) \\ \end{align} $
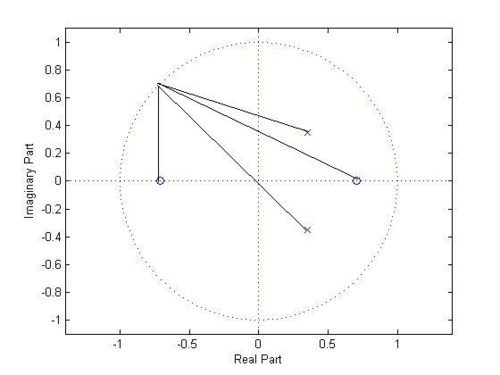
- Zero-pole plot
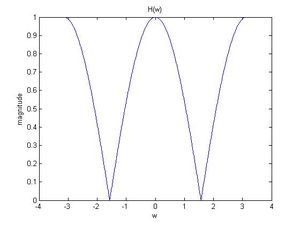
- Frequency response
b)
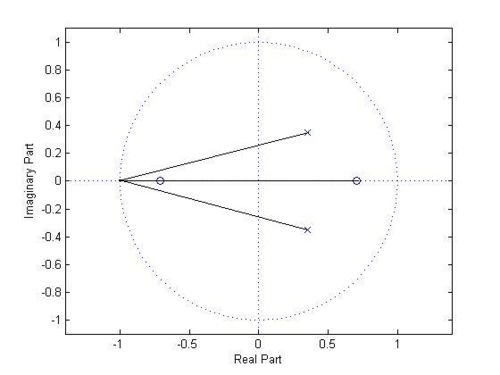
$ y[n]= \frac{x[n]-x[n-1]}{2} $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y[z]&= \frac{X[z]-X[z]z^{-1}}{2} \\ \frac{Y[z]}{X[z]}&= \frac{1-z^{-1}}{2} \\ H[z] &= \frac{1-z^{-1}}{2} \\ \end{align} $
Frequency Response $ H(\omega) $
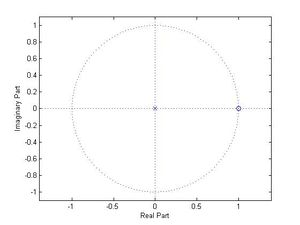
$ \begin{align} H[e^{j\omega }] &= \frac{1-e^{-j\omega }}{2} \\ &= e^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}-e^{-j\frac{\omega }{2}}}{2} \right) \\ &= je^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}-e^{-j\frac{\omega }{2}}}{2j} \right) \\ &= je^{-j\frac{\omega }{2}} sin \left( \frac{\omega }{2} \right) \\ \end{align} $
- Zero-pole plot
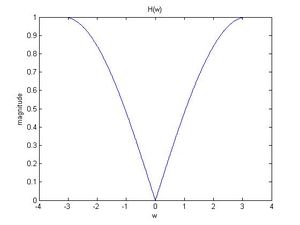
- Frequency response
Question 2
The frequency response is $ {\mathcal H}(\omega) = 1 + 2 e^{-j\omega } + e^{-2j\omega } $. Here are 5 different ways to compute it.
- Use pure frequency $ e^{j\omega_0 n} $ as an input; the output will be that same pure frequency $ e^{j\omega_0 n} $ multiplied by $ {\mathcal H}(\omega)_0 $.
- Set $ x[n]=\delta[n] $ to get the unit impulse response h[n] of the system. Then Fourier transform $h[n]$ to get the frequency response.
- Set $ x[n]=\delta[n] $ to get the unit impulse response h[n] of the system. Then z-transform $h[n]$ to get the transfer function of the system, and subsequently restrict the transfer function to the unit circle to get the frequency response.
- Take the Fourier transform of the left-hand-side and right-hand-side of the equation. Then use the fact that $ \frac{{\mathcal Y}(\omega)}{{\mathcal Y}(\omega)}={\mathcal H}(\omega) $ to get the frequency response of the system.
- Take the z-transform of the left-hand-side and right-hand-side of the equation. Then use the fact that $ \frac{Y(z)}{X(z)}=H(z) $ to get the transfer function of the system. Finally restrict the transfer function to the unit circle to get the frequency response.
Question 3
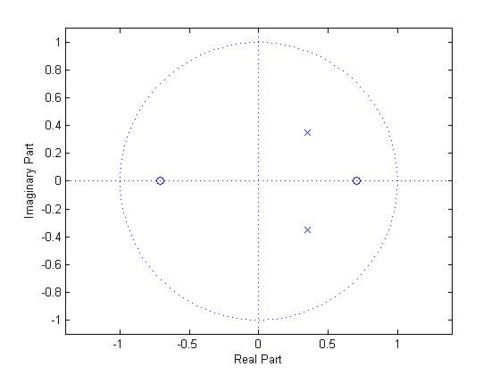
a. Sketch the locations of the poles and zeros.
$ \begin{align} H(z) &= \frac{1-\frac{1}{2}z^{-2}}{1-\frac{1}{\sqrt{2}} z^{-1} +\frac{1}{4} z^{-2}} \\ H(z) &= \frac{(z+\frac{1}{\sqrt{2}})(z-\frac{1}{\sqrt{2}})} { (z-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(z-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \\ \end{align} $
Zeros:
$ z_1 = \frac{1}{\sqrt{2}}, z_2 = -\frac{1}{\sqrt{2}} $
Poles:
$ p_1 = \frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}, p_2 = \frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}} $
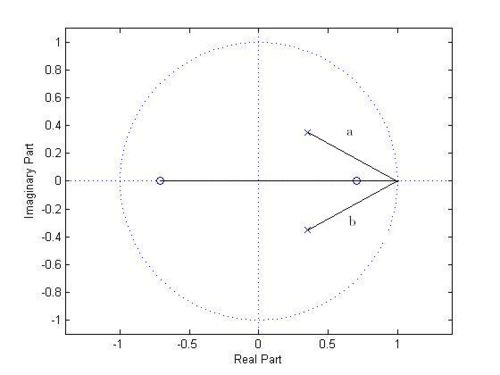
- b. Determine the magnitude and phase of the frequency response H(ω), for
$ \omega = 0 $
$ \left| H(e^{j\omega}) \right| = \left| H(e^{j0}) \right| = \left| H(z=1) \right| $
$ = \left| \frac{(1+\frac{1}{\sqrt{2}})(1-\frac{1}{\sqrt{2}})} { (1-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(1-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \right| = 0.921 $
$ \angle H(e^{j0}) = \angle c + \angle d - \angle a - \angle b = 0 $
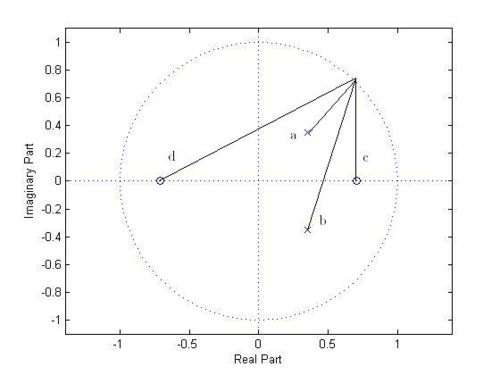
$ \omega =\frac{\pi}{4} $
$ \left| H(e^{j\omega}) \right| = \left| H(e^{j\frac{\pi}{4}}) \right| = \left| H(z=\frac{1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}) \right| $
$ = \left| \frac{(\frac{1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}})(\frac{1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}})} { (\frac{1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(\frac{1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \right| = 2 $
$ \angle H(e^{j\frac{\pi}{4}}) = \angle c + \angle d - \angle a - \angle b = \frac{\pi}{2} + arctan^{-1} \left( \frac{\frac{1}{\sqrt{2}}}{\sqrt{2}} \right) - \frac{\pi}{4} - arctan^{-1} \left( \frac{\frac{1}{\sqrt{2}} + \frac{1}{2\sqrt{2}}}{1-\sqrt{2}-\frac{1}{2\sqrt{2}}} \right) = 0 $
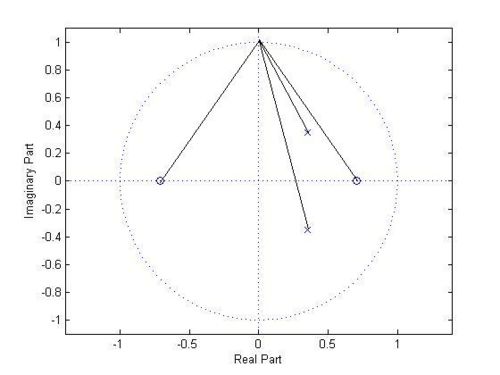
$ \omega =\frac{\pi}{2} $
$ \left| H(e^{j\omega}) \right| = \left| H(e^{j\frac{\pi}{2}}) \right| = \left| H(z=j) \right| $
$ = \left| \frac{(j+\frac{1}{\sqrt{2}})(j-\frac{1}{\sqrt{2}})} { (j-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(j-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \right| = 1.455 $
$ \angle H(e^{j\frac{\pi}{2}}) = (\angle c + \angle d) - \angle a - \angle b = (\pi) - (arctan^{-1}\left( \frac{1-\frac{1}{2\sqrt{2}}}{\frac{-1}{\sqrt{2}}} \right) + \pi) - (arctan^{-1}\left( \frac{1+\frac{1}{2\sqrt{2}}}{1-\frac{1}{\sqrt{2}}} \right) + \pi) = -0.7563 $
$ \omega =\frac{3\pi}{4} $
$ \left| H(e^{j\omega}) \right| = \left| H(e^{j\frac{3\pi}{4}}) \right| = \left| H(z=\frac{-1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}) \right| $
$ = \left| \frac{(\frac{-1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}})(\frac{-1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}})} { (\frac{-1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(\frac{-1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \right| = \frac{2}{3} $
$ \angle H(e^{j\frac{3\pi}{4}}) = \angle c + \angle d - \angle a - \angle b = (arctan^{-1}\left( \frac{\frac{1}{\sqrt{2}}}{\frac{-2}{\sqrt{2}}} \right) + \pi) + \frac{\pi}{2} - (arctan^{-1}\left( \frac{\frac{1}{\sqrt{2}} - \frac{1}{2\sqrt{2}}}{\frac{1}{\sqrt{2}} - \frac{1}{2\sqrt{2}}} \right) + \pi) + \frac{3\pi}{4} = -0.9273 $
$ \omega =\pi $
$ \left| H(e^{j\omega}) \right| = \left| H(e^{j\pi}) \right| = \left| H(z=-1) \right| $
$ = \left| \frac{(-1+\frac{1}{\sqrt{2}})(-1-\frac{1}{\sqrt{2}})} { (-1-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(-1-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \right| = 0.255 $
$ \angle H(e^{j\pi}) = (\angle c + \angle d) - \angle a - \angle b = 2\pi - 0 - 0 = 2\pi $
c. Is the system stable? Explain why or why not?
The system is causal and the ROC extends outwards from the outermost pole since |$ p_1 $| = |$ p_2 $| < 1 and this ROC contains the unit circle. Therefore the system is stable.
d. Find the difference equation for y[n] in terms of x[n], corresponding to this transfer function H(z).
$ H(z) = \frac{Y(z)}{X(z)} = \frac{1-\frac{1}{2}z^{-2}}{1-\frac{1}{\sqrt{2}} z^{-1} +\frac{1}{4} z^{-2}} $
$ Y(z)(1-\frac{1}{\sqrt{2}} z^{-1} +\frac{1}{4} z^{-2}) = X(z)(1-\frac{1}{2}z^{-2}) $
Taking inverse,
$ y[n]-\frac{1}{\sqrt{2}}y[n-1] + \frac{1}{4}y[n-2] = x[n] - \frac{1}{2}x[n-2] $
$ y[n] = x[n] - \frac{1}{2}x[n-2] +\frac{1}{\sqrt{2}}y[n-1] - \frac{1}{4}y[n-2] $
Question 4
$ y[n]=\frac{1}{8} \left( x[n]+x[n-1]+x[n-2]+x[n-3]+x[n-4]+x[n-5]+x[n-6]+x[n-7]\right) $
a.
$ h[n]=\frac{1}{8} \left( \delta[n]+\delta[n-1]+\delta[n-2]+\delta[n-3]+\delta[n-4]+\delta[n-5]+\delta[n-6]+\delta[n-7] \right) $
This is a finite duration response.
b.
$ H[z]=\frac{1}{8} \left( 1+z^{-1}+z^{-2}+z^{-3}+z^{-4}+z^{-5}+z^{-6}+z^{-7} \right) $
$ H[z]=\frac{1}{8} \left( \frac{1-z^{-8}}{1-z^{-1}} \right) $
c.
$ H[z]=\frac{1}{8} \left( \frac{z^{8}-1}{z^{7}(z-1)} \right) $
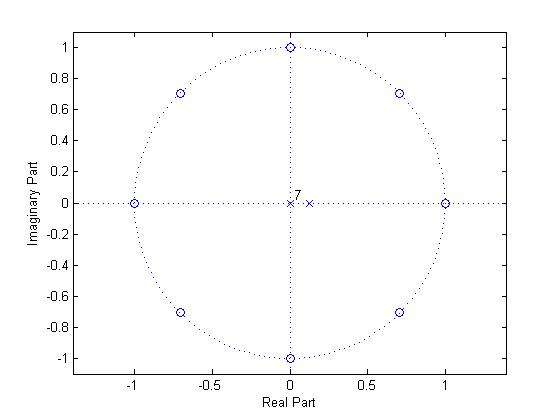
Poles:
$ p_1 = 1 $
$ p_2 = p_3 = ... = p_8 = 0 $
Zeros:
$ z^{8} - 1 = 0 $
$ z^{8} = e^{j2\pi } $
Generalizing,
$ z_k = e^{j2\pi k/8 } $ for k = 0,1,2,...,7
Question 5
a.
$ y[n]= \frac{1}{8} \left( x[n]-x[n-8]+y[n-1] \right) $
Using z-transform,
$ Y(z) = \frac{1}{8} \left( X(z)-X(z)z^{-8} + Y(z)z^{-1} \right) $
$ Y(z) (1 - \frac{1}{8}z^{-1}) = X(z) \frac{1}{8}(1 - z^{-8}) $
$ H(z) = \frac{Y(z)}{X(z)} = \frac{1}{8} \left( \frac{ 1 - z^{-8} } {1 - \frac{1}{8}z^{-1}} \right) $
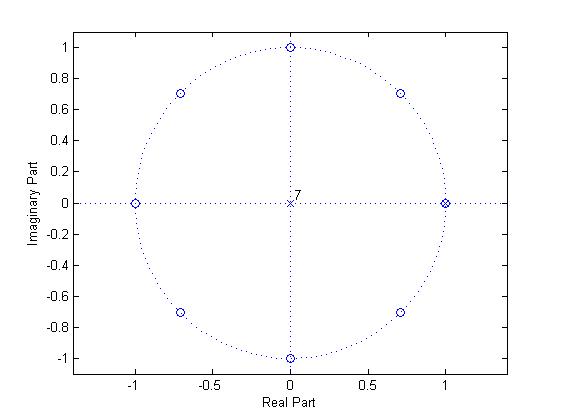
b.
c.
H(z) can be re-written as
$ H[z]=\frac{1}{8} \left( \frac{1}{1-\frac{1}{8}z^{-1}} - \frac{z^{-8}}{1-\frac{1}{8}z^{-1}} \right) $
Assuming the ROC: $ |z|>\frac{1}{8} $ Taking inverse Z-transform of H(z) -
$ h[n]=\frac{1}{8} \left( (\frac{1}{8})^n u[n] - (\frac{1}{8})^{n-8} u[n-8] \right) $
This is a infinite duration response.