(Added matching sections from google doc. Put in applications from google doc.) |
(Added computability and applications section from google doc.) |
||
| Line 43: | Line 43: | ||
'''Computability''' | '''Computability''' | ||
| + | |||
| + | The graph isomorphism problem is in NP. However, it has not been proven it is in NP-complete and a polynomial time algorithm has not been found. Many believe that the problem lies somewhere in between NP-Complete and P, although this has not been proven. | ||
| + | |||
| + | If the graph isomorphism problem was shown to be in NP but not in P nor NP-Complete it would automatically prove P is not equal to NP. | ||
| + | |||
| + | In 2015, László Babai from the University of Chicago presented an algorithm that has a quasi-polynomial time. If this finding is verified, the quasi-polynomial time would make the graph isomorphism much closer to P than NP-Complete, but still not in P. Babai himself speculated that the problem was very close to the boundary for the class P but not inside. | ||
'''Algorithms''' | '''Algorithms''' | ||
| + | |||
| + | Given two graphs A and B, in order for them to be isomorphic, every node in graph A must have a corresponding node in graph B such that given an edge between two nodes in graph A, there must be an edge between the corresponding nodes in graph B, and vice versa. The simplest way to demonstrate isomorphism between two graphs would be to construct a list of corresponding nodes. One method for constructing this list would be to use adjacency matrices. Given that graphs A and B have n nodes, the following steps should show whether or not they are isomorphic: | ||
| + | |||
| + | # Label the nodes of graph A as 1 through n and construct an adjacency matrix for A. | ||
| + | # Label the nodes of graph B as 1 through n and construct an adjacency matrix for B. | ||
| + | # Compare the adjacency matrices for A and B. If they are identical, A and B are isomorphic. If they are not, go back to step 2, labeling the nodes differently. | ||
| + | # If all the possible numberings of graph B have been exhausted and no match has been found, A and B are not isometric. | ||
| + | |||
| + | While this method might work well for small graphs, this method quickly takes unmanageably long to compute as the size of graphs A and B increase. Specifically, any brute force method such as this one takes (at most) n! comparisons. Although this algorithm will consistently return the correct answer, for practical reasons it is unusable. | ||
| + | |||
| + | For several special cases (mentioned below) it is possible to determine the isomorphism of a graph more efficiently than by using a brute-force, factorial runtime algorithm. However, no general algorithm exists yet that can determine isomorphism between two graphs in polynomial time. | ||
'''History''' | '''History''' | ||
Revision as of 14:06, 24 April 2016
Group A: The Graph Isomorphism Problem
The Graph Isomorphism Problem
Introduction
The graph isomorphism problem has been a long-standing problem in complexity theory for the last four decades. The statement of the problem is fairly simple: Given any two finite graphs that may appear to be different, is there an "easy" way to tell whether or not the two graphs are the same? We'll look at the statement of the problem in a slightly more rigorous setting, discuss the importance of the problem in other fields, as well as some recent progress made on the problem by a professor at the University of Chicago.
Basic concepts
We'll start off with some basic concepts related to the problem and formulate a more rigorous statement of the problem.
$ \ \text{Definitions} $
• A $ \ \text{Graph } G $ is a pair of sets $ \ G = (E_{G}, V_{G}) $ , where $ \ V_{G} $ is the set of vertices (or "dots") in the graph and $ \ E_{G} $ is the set of edges (or "lines") for the graph.
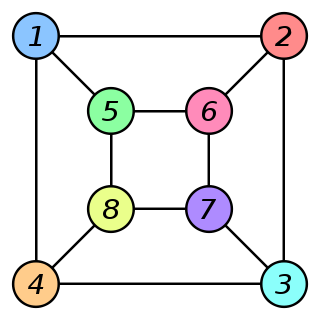
• A $ \ \text{Graph Isomorphism } f $ between two graphs $ \ G \text{ and } H $ is a bijective function $ \ f : V_{G} \rightarrow V_{H} $ with the property that there is an edge between $ \ v_{i} \text{ , } v_{j} \in V_{G} $ if and only if there is an edge between $ \ f(v_{i}) \text{ , } f(v_{j}) \in V_{H} $ . In other words, this is a one-one correspondence between $ \ G \text{ and } H $ showing that they are in fact the same graph. One example of a graph isomorphism is the following:
Applications
Isomorphic graphs have a lot of applications nowadays. All the entities in the world can be represented by some sort of connections. A big part of today's technology is to figure out these connections and relations. Every time when we show an isomorphism between such relations with graphs, a new star starts to shine on the firmament of human thinking power.
Listed below are some of the more concrete areas that use graph isomorphism:
- In automata theory. There are multiple uses. The main one is to show that some two languages are equal.
- In parallel processing: to reason about behavior of complex systems.
- In verification of things: e.g. computer programs, logic proofs, or even electronic circuits.
- In compilers. e.g. perform optimizations.
- In search engines that use formulas more sophisticated than words. e.g. in biology DNA structures.
- Security. e.g. fingerprints scanners, facial scanners, and retina scanners.
- Civil engineering, city planning, building interior planning (e.g. recognizing geographic locations with desired properties).
- Analysis of social structures (special cases may include schools, military, parties, events, etc.).
- Analysis of business relations.
- Any system that performs clustering would benefit from fast graph-isomorphism algorithm, e.g.
* linking two Facebook accounts of the same person
* recognizing web users based on their behavior
* recognizing plagiarism in students solutions
Computability
The graph isomorphism problem is in NP. However, it has not been proven it is in NP-complete and a polynomial time algorithm has not been found. Many believe that the problem lies somewhere in between NP-Complete and P, although this has not been proven.
If the graph isomorphism problem was shown to be in NP but not in P nor NP-Complete it would automatically prove P is not equal to NP.
In 2015, László Babai from the University of Chicago presented an algorithm that has a quasi-polynomial time. If this finding is verified, the quasi-polynomial time would make the graph isomorphism much closer to P than NP-Complete, but still not in P. Babai himself speculated that the problem was very close to the boundary for the class P but not inside.
Algorithms
Given two graphs A and B, in order for them to be isomorphic, every node in graph A must have a corresponding node in graph B such that given an edge between two nodes in graph A, there must be an edge between the corresponding nodes in graph B, and vice versa. The simplest way to demonstrate isomorphism between two graphs would be to construct a list of corresponding nodes. One method for constructing this list would be to use adjacency matrices. Given that graphs A and B have n nodes, the following steps should show whether or not they are isomorphic:
- Label the nodes of graph A as 1 through n and construct an adjacency matrix for A.
- Label the nodes of graph B as 1 through n and construct an adjacency matrix for B.
- Compare the adjacency matrices for A and B. If they are identical, A and B are isomorphic. If they are not, go back to step 2, labeling the nodes differently.
- If all the possible numberings of graph B have been exhausted and no match has been found, A and B are not isometric.
While this method might work well for small graphs, this method quickly takes unmanageably long to compute as the size of graphs A and B increase. Specifically, any brute force method such as this one takes (at most) n! comparisons. Although this algorithm will consistently return the correct answer, for practical reasons it is unusable.
For several special cases (mentioned below) it is possible to determine the isomorphism of a graph more efficiently than by using a brute-force, factorial runtime algorithm. However, no general algorithm exists yet that can determine isomorphism between two graphs in polynomial time.
History
Special Cases