(Almost done) |
|||
| Line 35: | Line 35: | ||
'''Tournaments''' | '''Tournaments''' | ||
| − | [[File:Roundrobin.png|500px|thumb| | + | When discussing tournaments, the following assumptions about transitivity, wins and losses, and draws must be considered. In a transitive tournament if Player A beats Player B and Player B beats Player C, then Player A beats Player C. For every two players, Player A beats Player B, else Player B beats Player A, i.e. there are no draws. For this project, we are examining single elimination and round robin tournaments. |
| + | |||
| + | # Single Elimination: In a single elimination tournament, a team is eliminated from the tournament immediately after it loses a contest. Then the winners of the previous rounds game play each other until two teams are left. The winner of the final game is the winner of the tournament. The number of teams t must be equal to a power of 2, defined to be t = 2^n for n = 1,2,3… For example, a single-elimination tournament could have 4, 8, or 16 teams. If t =/ 2^n, n =1, 2, 3, you will have to select a portion of the team. For example, if a single elimination tournament is being conducted for a league of 36 teams, the tournament coordinate might select only the top 32 teams to participate, since 32 = 2^5. | ||
| + | # Round Robin: | ||
| + | * N teams, N-1 rounds,A round robin tournament with N players will consist of N-1 rounds. | ||
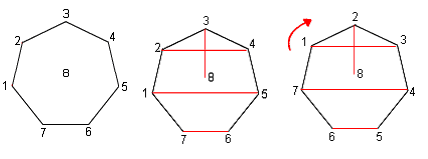
| + | * Refer to the figure below.Draw a regular polygon with N-1 vertices if N is even or N vertices if N is odd. Assign a team to each node and one to the center if N is even. Draw horizontal lines connecting opposite nodes and a vertical line from the top node to the center node. Each line represents a match in the round.after that round simply rotate the polygon about the center so that the nodes match up again. Repeat this step until all teams have played each other. This should be N-1 rotations. | ||
| + | |||
| + | |||
| + | [[File:Roundrobin.png|500px|thumb|center|]] | ||
| + | |||
| + | '''Example:''' | ||
| + | '''''March Madness''''' | ||
| + | |||
| + | The NCAA Men’s Division 1 Basketball Tournament is the championship competition among 68 college basketball teams, commonly referred to as March Madness. Teams qualify by either being one of the top 32 Division 1 automatic qualifiers, or is one of 36 teams selected by the NCAA Tournament Committee to fill the remaining spots. Then the committee seeds the teams 1 through 68 and places them in the bracket according to this order. There are four regions, and seeds 1-4 are placed one in each region. This process extends until the bracket is full, resulting in 64 teams. Thus 64 = 2^6 and we are able to complete a single elimination tournament. Eliminations result in significant rounds, each of which is a power of 2: Sweet Sixteen (2^4), Elite Eight (2^3), and Final Four (2^2). The Final Four consists of the winner of each region of the bracket. | ||
| + | |||
| − | |||
| Line 44: | Line 57: | ||
In conclusion, we see that the graphical theory behind tournaments is not too far separated from traditional graph theory. Tournament theory has been very significant over time in finding ways to fairly determine a winner among several teams in competition. Two main methods for doing so, Single Elimination and Round Robin, arose. The advantages of Single Elimination are that it is a short and uncomplicated design, and eliminates half of the participants at each round. However, the main disadvantage is the “luck” component where one bad round completely eliminates a team and can be unreflective of a team’s overall skill level. Round Robin addresses this concern because every team must play every other team; however, the time and coordination required for this is much greater than that for Single Elimination. Once again, in math we find ourselves at the crossroads of efficiency and equality. The most surprising part is that there is a type of tournament where a clear winner, which is the original reason tournament theory came about. These types of tournaments are called paradoxical tournaments. For further information about tournaments | In conclusion, we see that the graphical theory behind tournaments is not too far separated from traditional graph theory. Tournament theory has been very significant over time in finding ways to fairly determine a winner among several teams in competition. Two main methods for doing so, Single Elimination and Round Robin, arose. The advantages of Single Elimination are that it is a short and uncomplicated design, and eliminates half of the participants at each round. However, the main disadvantage is the “luck” component where one bad round completely eliminates a team and can be unreflective of a team’s overall skill level. Round Robin addresses this concern because every team must play every other team; however, the time and coordination required for this is much greater than that for Single Elimination. Once again, in math we find ourselves at the crossroads of efficiency and equality. The most surprising part is that there is a type of tournament where a clear winner, which is the original reason tournament theory came about. These types of tournaments are called paradoxical tournaments. For further information about tournaments | ||
| + | '''References''' | ||
| + | |||
| + | [1] Glickenstein, David. Math 443/543 Graph Theory Notes 6: Digraphs, Traffic, and Tournaments (2008): 1-3. 9 Sept. 2008. Web. 22 Apr. 2016. | ||
| + | |||
| + | [2] NCAA.com. “March Madness bracket: How the 68 teams are selected for the Division I Men’s Basketball Tournament.” NCAA.org. Web. 22 Apr. 2016. | ||
| + | |||
| + | [3] "Tournament (graph Theory)." Wikipedia. Wikimedia Foundation, 18 Apr. 2015. Web. 22 Apr. 2016. | ||
| + | |||
| + | [4] Weisstein, Eric W. "Tournament." Wolfram MathWorld. From MathWorld--A Wolfram Web Resource, n.d. Web. 22 Apr. 2016. | ||
| + | |||
| + | [5] Y, Arunachalam. "Tournament Scheduling." : Nrich.maths.org. NRICH, Jan. 2012. Web. 22 Apr.2016. | ||
[[Category:MA279Spring2016Walther]] | [[Category:MA279Spring2016Walther]] | ||
Revision as of 14:11, 23 April 2016
Scheduling MA 279 Team Project: Dana Smith, Bronz McDaniels, Ryan Andrew, Eliot Mathieu
Introduction
The mathematics of tournaments refers to the use of digraphs, where vertices represent teams or players, and arcs between vertices indicate the winner and loser of each game played in the tournament. Games cannot end in a tie. Types of tournaments include single elimination and round robin.
Definitions
The following vocabulary is necessary and useful for understanding the mathematics of tournaments.
- Tournament: A tournament T is an orientation of a complete graph. Thus for every pair of vertices v, w in T, either (v, w) or (w,v) is an arc of the graph.
- Digraph: A graph in which the edges have a direction associated to them, typically indicated by an arrow
- Arcs: A directed edge that is defined by a starting vertex and its ending vertex. If we have vertices X and Y we will define XY as an arc in which X goes to Y
- Arc-set: A list of all the arcs in a digraph.
- Indegree: The indegree of a vertex X is the number of arcs that have X as their ending point.
- Outdegree: The outdegree of a vertex X is the number of arcs that have X as their starting point.
- Complete graph:A graph with N vertices in which every pair of distinct vertices is joined by an edge. Denoted by the symbol Kn.
- Paths: A sequence of arcs that are adjacent to one another. For example the arcs XY,YZ,ZA,AC would be a path from vertex X to vertex C. For simplicity we will denote a path by the sequence of vertices that connects (X,Y,Z,A,C).
- Cycle: A path that starts and ends at the same vertex.
- Score sequence: The set of scores that each player would receive in the tournament, where each win counts as one point and a loss counts as no points. This is achieved by sorting the set of outdegrees in nondecreasing order.
Tournaments
When discussing tournaments, the following assumptions about transitivity, wins and losses, and draws must be considered. In a transitive tournament if Player A beats Player B and Player B beats Player C, then Player A beats Player C. For every two players, Player A beats Player B, else Player B beats Player A, i.e. there are no draws. For this project, we are examining single elimination and round robin tournaments.
- Single Elimination: In a single elimination tournament, a team is eliminated from the tournament immediately after it loses a contest. Then the winners of the previous rounds game play each other until two teams are left. The winner of the final game is the winner of the tournament. The number of teams t must be equal to a power of 2, defined to be t = 2^n for n = 1,2,3… For example, a single-elimination tournament could have 4, 8, or 16 teams. If t =/ 2^n, n =1, 2, 3, you will have to select a portion of the team. For example, if a single elimination tournament is being conducted for a league of 36 teams, the tournament coordinate might select only the top 32 teams to participate, since 32 = 2^5.
- Round Robin:
- N teams, N-1 rounds,A round robin tournament with N players will consist of N-1 rounds.
- Refer to the figure below.Draw a regular polygon with N-1 vertices if N is even or N vertices if N is odd. Assign a team to each node and one to the center if N is even. Draw horizontal lines connecting opposite nodes and a vertical line from the top node to the center node. Each line represents a match in the round.after that round simply rotate the polygon about the center so that the nodes match up again. Repeat this step until all teams have played each other. This should be N-1 rotations.
Example: March Madness
The NCAA Men’s Division 1 Basketball Tournament is the championship competition among 68 college basketball teams, commonly referred to as March Madness. Teams qualify by either being one of the top 32 Division 1 automatic qualifiers, or is one of 36 teams selected by the NCAA Tournament Committee to fill the remaining spots. Then the committee seeds the teams 1 through 68 and places them in the bracket according to this order. There are four regions, and seeds 1-4 are placed one in each region. This process extends until the bracket is full, resulting in 64 teams. Thus 64 = 2^6 and we are able to complete a single elimination tournament. Eliminations result in significant rounds, each of which is a power of 2: Sweet Sixteen (2^4), Elite Eight (2^3), and Final Four (2^2). The Final Four consists of the winner of each region of the bracket.
Conclusion
In conclusion, we see that the graphical theory behind tournaments is not too far separated from traditional graph theory. Tournament theory has been very significant over time in finding ways to fairly determine a winner among several teams in competition. Two main methods for doing so, Single Elimination and Round Robin, arose. The advantages of Single Elimination are that it is a short and uncomplicated design, and eliminates half of the participants at each round. However, the main disadvantage is the “luck” component where one bad round completely eliminates a team and can be unreflective of a team’s overall skill level. Round Robin addresses this concern because every team must play every other team; however, the time and coordination required for this is much greater than that for Single Elimination. Once again, in math we find ourselves at the crossroads of efficiency and equality. The most surprising part is that there is a type of tournament where a clear winner, which is the original reason tournament theory came about. These types of tournaments are called paradoxical tournaments. For further information about tournaments
References
[1] Glickenstein, David. Math 443/543 Graph Theory Notes 6: Digraphs, Traffic, and Tournaments (2008): 1-3. 9 Sept. 2008. Web. 22 Apr. 2016.
[2] NCAA.com. “March Madness bracket: How the 68 teams are selected for the Division I Men’s Basketball Tournament.” NCAA.org. Web. 22 Apr. 2016.
[3] "Tournament (graph Theory)." Wikipedia. Wikimedia Foundation, 18 Apr. 2015. Web. 22 Apr. 2016.
[4] Weisstein, Eric W. "Tournament." Wolfram MathWorld. From MathWorld--A Wolfram Web Resource, n.d. Web. 22 Apr. 2016.
[5] Y, Arunachalam. "Tournament Scheduling." : Nrich.maths.org. NRICH, Jan. 2012. Web. 22 Apr.2016.