| Line 63: | Line 63: | ||
* Step 5 On the original graph add the edges that have been found in Step 4. (See following graph) | * Step 5 On the original graph add the edges that have been found in Step 4. (See following graph) | ||
[[File: example1forchinesepostmanproblemmodified.jpg]] | [[File: example1forchinesepostmanproblemmodified.jpg]] | ||
| − | * Step 6 | + | * Step 6 Total weight should be 79+19=98. |
| − | * Step 7 A route | + | * Step 7 A possible route of this weight can be AFEDFEDCFBCBA |
Revision as of 02:09, 23 April 2016
Contents
Chinese postman problem
Introduction
(Sargun)
The Chinese postman problem, also known as the route inspection problem, is to find a circuit in a connected, undirected graph that visits each edge at least once. Additionally, a correct solution minimizes the total cost of the circuit. If all vertices of the graph have even degree, then the optimal solution is the Euler circuit of the graph. In this case, the cost of the solution is the sum of all edge weights in the graph.
In the case where the graph has some odd edges, the solution is more complicated. First, identify all nodes with odd degree. Next, pair up the odd nodes such that the sum of the weights of the shortest paths between pairs is a minimum. Then, take all the edges from the paths in the previous step, and duplicate them. This ensures that all nodes now have even degree, while adding the minimum possible weight to the graph. Finally, the solution is the Euler circuit of the modified graph, and the cost is the sum of all edge weights in the original graph plus the sum of the weights of the duplicated edges.
(TODO Analysis)
History
(Hao Xu)
During the Great Leap Forward movement period in the Chinese history (1958-1960), president Mao of China encouraged scientists to solve real-world problems in order to accelerate the transformation of economy mode of China. At that time, many mathematics researchers focused on problems like transportation and production planning. And Shandong province, as a center of early Chinese mathematics researches, is where Chinese Postman Problem was created. (Grotschel & Yuan, 2010).
Chinese Postman Problem was discovered by a Chinese mathematician --- Kwan Mei-Ko. The problem described a situation that the Chinese postman would face everyday. The exact problem was defined in Kwan's paper as, "A postman has to deliver letters to a given neighborhood. He needs to walk through all the streets in the neighborhood and back to the post-office. How can he design his route so that he walks the shortest distance?"
Then he converted this problem to a more generic one by counting the number of edges linked to a node as, "Given a connected graph where 2n of the nodes are odd and all other nodes are even. Suppose we need to add some edges to the graph with the following property: the number of edges added to any odd node is odd and that added to any even node is even. We need to minimize the total length of the added edges."
Then he solved this problem by his theorem, which is also in his paper, "For a set of added edges it is necessary and sufficient to be an optimal solution for the above problem if the following two conditions hold: 1). Between any two nodes, no more than one edge is added, 2). In any cycle of the extended graph, the total length of the added edge is not greater than half of the total length of the cycle."
Real-world applications
(Zexuan Zhou)
An early example of application is that a postman delivering letters in a village may wish to know a circuit that traverses each street (to minimize the total traveled distance), starting and returning to their office. (Thimbleby, 2003) This is a graph theoretic problem: roads are connected edges, and the joint point of streets are vertices. The postman requires a Chinese Postman Tour(CPT).
Conventional applications of the Chinese Postman Problem (CPP) are concerned with routing in a more general way, as in planing snow ploughs or street maintenance. Nowadays, the CPP and CPT are more widely used in network algorithm checking.
Imagine trying to understand your mobile phone. Pressing buttons takes the phone to a new state, and corresponds to travelling an "edge". After some considerable work, one might obtain a map of how the phone works. However one don't know if the map is correct or not, and the map may be difficult and complex to test systematically. Given the map, a CPT will provide a systematic test sequence that will exercise each transition. (Thimbleby, 2003) As a concrete example, the Nokia 2110 mobile phone has a menu subsystem of 88 menu-items and 274 actions (Nokia 2110 User's Guide, 1996). The optimal CPT takes 515 button presses plus 79 presses to check presses that has no functional ability. In comparison, the shortest trip that visits each vertex at least once, to check that each menu item function corresponds correctly to its name, is only 98 button presses. (Thimbleby, 2003) This is much easier to check the functionality.
Another example is the mobile robot exploration problem, where a robot has to explore a network by exploring every edge and vertex of the network before it know the entire map. For a network of m arcs, an algorithm has been found that takes at most mφ^O(log φ) steps, where φ is the deficiency of the graph, which is a measure of the ease o use of a system. (Albers & Henzinger, 1997) We will see that the algorithm for the CPT also determines the deficiency. (Thimbleby, 2003)
Variations
(Evan)
Examples
(Hao Wu)
Chinese Postman Algorithm (Pearson, 2004)
- Step 1 List all odd vertices.
- Step 2 List all possible pairings of odd vertices.
- Step 3 For each pairing find the edges that connect the vertices with the minimum weight.
- Step 4 Find the pairings such that the sum of the weights is minimized.
- Step 5 On the original graph add the edges that have been found in Step 4.
- Step 6 The length of an optimal Chinese postman route is the sum of all the edges added to the total found in Step 4.
- Step 7 A route corresponding to this minimum weight can then be easily found.
We will apply the above algorithm in the following example to find a minimum Chinese postman route in each case.
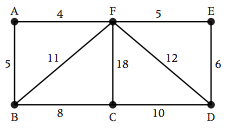
- Step 1 B, C, F and D are odd vertices.
- Step 2 BC-FD, BF-CD and BD-CF are possible pairings of odd vertices.
- Step 3 For each pairing find the edges that connect the vertices with the minimum weight: BC-FD: 8+11=19. BF-CD: 9+10=19. BD-CF: 17+18=35.
- Step 4 Find the pairings such that the sum of the weights is minimized: BC-FD and BF-CD.
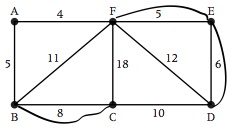
- Step 5 On the original graph add the edges that have been found in Step 4. (See following graph)
- Step 6 Total weight should be 79+19=98.
- Step 7 A possible route of this weight can be AFEDFEDCFBCBA
References
Kwan, M. K. (1960). Programming method using odd or even pints, Acta Mathematica sinica, 10, 263-266.
Grotschel, M., & Yuan, Y. X. (2010). Euler, Mei-ko Kwan, Konigsberg, and a Chinese postman. Documenta Math., 43-50.
Nokia Mobile Phones, Nokia 2110 User’s Guide, Issue 5, 1996.
S. Albers & M. R. Henzinger, Exploring Unknown Environments, Digital Systems Research Center, SRC Technical Note 1997-014, 1997.
H. Thimbleby, The Directed Chinese Postman Problem, Practice and Experience, 2003, Vol.33(11), pp.1081-1096.
Pearson, David. (2004) Decision Maths 1. London : Heinemann.