| Line 31: | Line 31: | ||
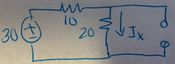
Let's find <math> I_x </math> first by deactivating the voltage source as seen in the picture below. | Let's find <math> I_x </math> first by deactivating the voltage source as seen in the picture below. | ||
| − | [[File: | + | [[File:ECE201 2.jpg|175px|center]] |
We can find <math> I_x </math> by using loop analysis. The left loop can be <math> I_1 </math> and the right loop can be <math> I_2 </math>.<br /> | We can find <math> I_x </math> by using loop analysis. The left loop can be <math> I_1 </math> and the right loop can be <math> I_2 </math>.<br /> | ||
When doing loop analysis we can come up with the following equation:<br /> | When doing loop analysis we can come up with the following equation:<br /> | ||
| Line 63: | Line 63: | ||
<math>\begin{align} | <math>\begin{align} | ||
I_x = \frac{1/10}{1/10 + 1/20} * 3\\ | I_x = \frac{1/10}{1/10 + 1/20} * 3\\ | ||
| + | |||
I_x = 2\\ | I_x = 2\\ | ||
\end{align} | \end{align} | ||
| Line 68: | Line 69: | ||
Finally, the last step would be to add up the two <math> I_x </math><br /> we obtained by deactivating the voltage and current sources. | Finally, the last step would be to add up the two <math> I_x </math><br /> we obtained by deactivating the voltage and current sources. | ||
| − | <math> I_x = -1 + 2</math> | + | <math> I_x = -1 + 2</math><br /> |
| − | <math> I_x = 1A</math> | + | <math> I_x = 1A</math><br /> |
Revision as of 15:23, 2 May 2015
Superposition Practice
Practice question for ECE201: "Linear circuit analysis I"
By: Chinar Dhamija
Topic: Superposition
Question
Determine the value of $ I_x $ using superposition.
Answer
The circuit has two sources, a voltage and a current source. In order to find $ I_x $ we need to look at two instances.
1. Deactivate the voltage source (V = 0)
2. Deactivate the current source (I = 0)
Let's find $ I_x $ first by deactivating the voltage source as seen in the picture below.
We can find $ I_x $ by using loop analysis. The left loop can be $ I_1 $ and the right loop can be $ I_2 $.
When doing loop analysis we can come up with the following equation:
$ \begin{align} I_1:\\ 10*I_1 + 20(I_1 - I_2) = 0\\ 30*I_1 = 20*I_2\\ I_2:\\ I_2 = 3A\\ \end{align} $
After finding $ I_1 $ and $ I_2 $ we can find $ I_x $. $ \begin{align} I_x = I_1 - I_2\\ I_x = 2 - 3\\ I_x = -1\\ \end{align} $
That is what we get for $ I_x $ if the voltage source is deactivated.
Now we need to do the same procedure but this time we will deactivate the current source; therefore, we will get the following circuit:
We can use source transformation to turn the voltage source into the current then use current division to solve for $ I_x $.
After doing source transformation we get the following circuit:
Now use current division to find $ I_x $.
$ \begin{align} I_x = \frac{1/10}{1/10 + 1/20} * 3\\ I_x = 2\\ \end{align} $
Finally, the last step would be to add up the two $ I_x $
we obtained by deactivating the voltage and current sources.
$ I_x = -1 + 2 $
$ I_x = 1A $
Questions and comments
If you have any questions, comments, etc. please post them below
- Comment 1
- Answer to Comment 1
- Comment 2
- Answer to Comment 2