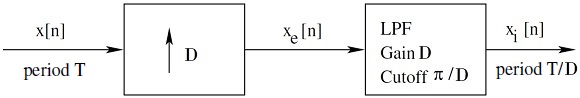| Line 31: | Line 31: | ||
<math> | <math> | ||
| − | + | x_i(n) = | |
\begin{cases} | \begin{cases} | ||
x(n/D), & n/D \text{ is an integer} \\ | x(n/D), & n/D \text{ is an integer} \\ | ||
| Line 42: | Line 42: | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| − | \ | + | \ X_i(e^{j\omega}) &= \sum_{n} x(n/D)e^{-j\omega n} \\ |
&= \sum_{n} s_D(n)x(n/D)e^{-j\omega n} \\ | &= \sum_{n} s_D(n)x(n/D)e^{-j\omega n} \\ | ||
\end{align} | \end{align} | ||
| Line 51: | Line 51: | ||
</math> | </math> | ||
| − | <math> | + | <center><math> |
\begin{align} | \begin{align} | ||
| − | \ | + | \ X_i(e^{j\omega}) &= \sum_{m} s_D(mD)x(m)e^{-j\omega mD} \\ |
\end{align} | \end{align} | ||
| − | </math> | + | </math></center> |
<math> | <math> | ||
| Line 61: | Line 61: | ||
</math> | </math> | ||
| − | <math> | + | <center><math> |
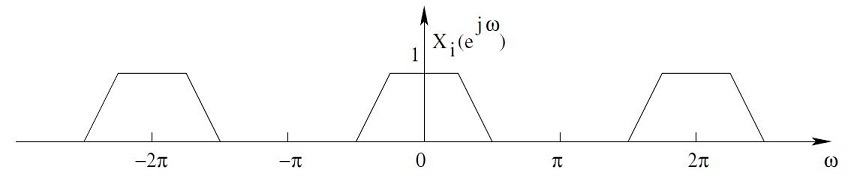
| − | \therefore | + | \therefore X_i(e^{j\omega}) = X(e^{j\omega D}) |
| − | </math> | + | </math></center> |
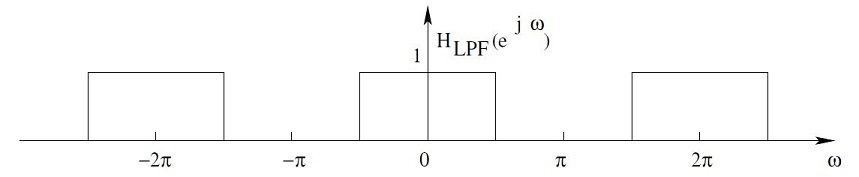
==Interpolator== | ==Interpolator== | ||
To interpolate between the nonzero saples generated by upsampling, a low pass filter is used. So the combiation of an upsanpler followed by a low pass filter can be referred to as an interpolator. | To interpolate between the nonzero saples generated by upsampling, a low pass filter is used. So the combiation of an upsanpler followed by a low pass filter can be referred to as an interpolator. | ||
| − | |||
| − | |||
---- | ---- | ||
==3. Examples== | ==3. Examples== | ||
| + | Graphical Representation | ||
| + | <center>[[Image:interpolator_1.jpg]]</center> | ||
| + | <center>[[Image:example_1.jpg]]</center> | ||
| + | <center>[[Image:example_2.jpg]]</center> | ||
| + | <center>[[Image:example_3.jpg]]</center> | ||
| + | <center>[[Image:example_4.jpg]]</center> | ||
Revision as of 10:10, 13 October 2014
Frequency Domain View of Upsampling
A slecture by exchange student from UNAM, Mexico, Michel Olvera.
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
OUTLINE
- Introduction
- Theory
- Examples
- Conclusion
- References
1. Introduction
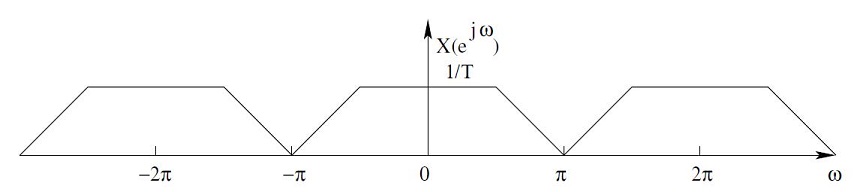
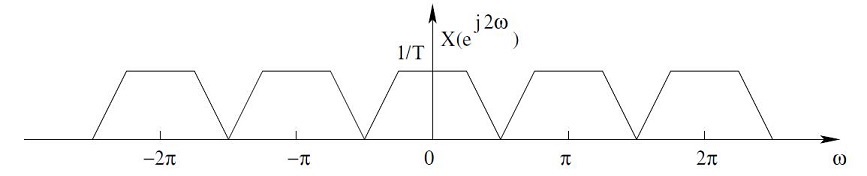
Upsampling is the process of inserting zero-valued samples between the original samples of a signal to increase the sampling rate. One way to accomplish upsampling by an integer ratio of 1:D is to interpose D-1 zero samples between each pair of the input samples of the signal. This causes the spectrum of the original signal to repeat at multiples of the original sampling rate.
The process of upsampling doesn’t change the content of the input signal, and it only introduces the scaling of the time axis by a factor D. Consequently, the operation of upsampling is invertible, which means that it is possible to recover the input signal from samples of the output exactly.
In order to remove or at least attenuate the unwanted image spectra, a low pass filter must be placed immediately after upsampling. In the time domain, the effect is that the zero-valued samples introduced by the upsampler are filled with interpolated values.
2. Theory
$ x_i(n) = \begin{cases} x(n/D), & n/D \text{ is an integer} \\ 0, & \text{otherwise} \end{cases} $
$ \begin{align} \ X_i(e^{j\omega}) &= \sum_{n} x(n/D)e^{-j\omega n} \\ &= \sum_{n} s_D(n)x(n/D)e^{-j\omega n} \\ \end{align} $
$ \text{Let } m=n/D \Rightarrow n=mD $
$ \text{But } s_D(mD) \equiv 1 $
Interpolator
To interpolate between the nonzero saples generated by upsampling, a low pass filter is used. So the combiation of an upsanpler followed by a low pass filter can be referred to as an interpolator.
3. Examples
Graphical Representation