| Line 17: | Line 17: | ||
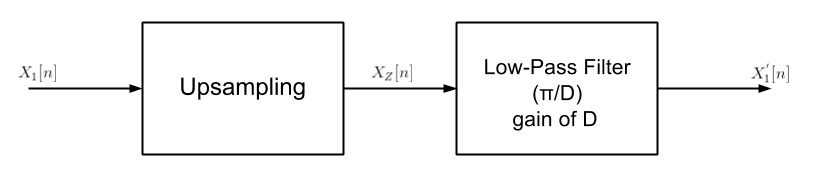
<br> [[Image:Block.jpg]] <br> | <br> [[Image:Block.jpg]] <br> | ||
| − | '''Theory'''<br> Upsampling in the frequency domain. It can be obtain in two different ways.<br> <br> [[Image:Theroy.jpg]] '''or ''' [[Image:CodeCogsEqn.jpg]] | + | '''Theory'''<br> Upsampling in the frequency domain. It can be obtain in two different ways.<br> <br> [[Image:Theroy.jpg]] '''or ''' [[Image:CodeCogsEqn.jpg]]<br> |
| − | + | ||
| − | <br> | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
<br> | <br> | ||
Revision as of 07:49, 10 October 2014
OUTLINE
1. Introduction
2. Theory
3. Example
4. Conclusion
_________________________________________________________________________________________________________
Introduction
Upsampling is the process of increasing sampling rate of discret-time signal. In this slecture, I will discuss about how it works and example of upsampling.
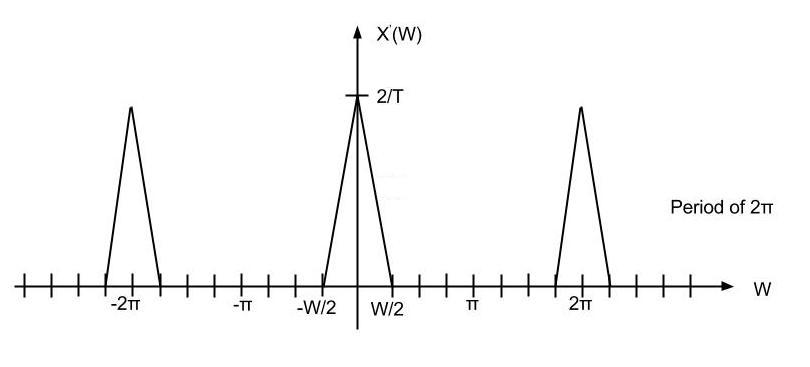
Theory
Upsampling in the frequency domain. It can be obtain in two different ways.
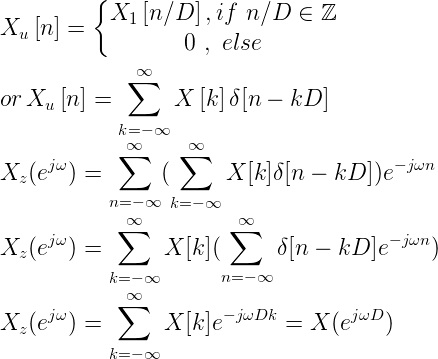 or
or 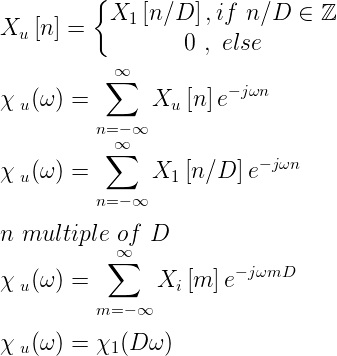
Example
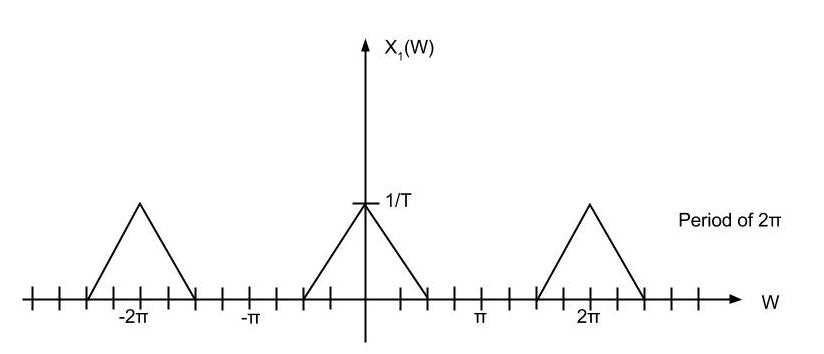
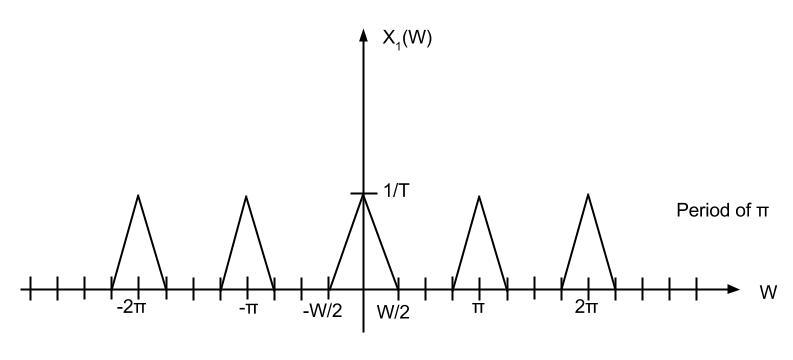
Upsampling rate D = 2
Here is the example of sampled signal.
Upsampling rate D = 2 is applied.
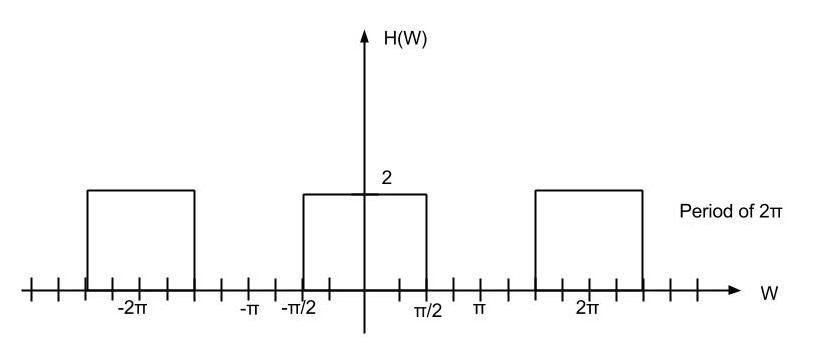
Low-Pass filter of cutoff π/2, gain 2 is applied.
Here is the final upsampled signal.
Conclusion
Upsampling by D inserts D - 1 zeros between every element of the original signal. Upsampling can create imaging artifacts. Lowpass filtering following upsampling can remove these imaging artifacts. In the time domain, lowpass filtering interpolates the zeros inserted by upsampling.