| Line 21: | Line 21: | ||
</math> The comb of a signal is equal to the signal multiplied by an impulse train. <math> | </math> The comb of a signal is equal to the signal multiplied by an impulse train. <math> | ||
\begin{align} | \begin{align} | ||
| − | X_s(f) &= F(x_s(t)) = F(comb_T)\\ | + | X_s(f) &= F(x_s(t)) = F(comb_T(x(t))\\ |
&= F(x(t)p_T(t))\\ | &= F(x(t)p_T(t))\\ | ||
&= X(f) * F(p_T(f)\\ | &= X(f) * F(p_T(f)\\ | ||
Revision as of 20:42, 6 October 2014
Outline
Introduction
Derivation
Example
Conclusion
Introduction
Hello! My name is Ryan Johnson! You might be wondering what a slecture is! A slecture is a student lecture that gives a brief overview about a particular topic! In this slecture, I will discuss the relationship between an original signal and a sampling of that original signal. We will also take a look at how this relationship translates to the frequency domain.
Derivation
F = fourier transform
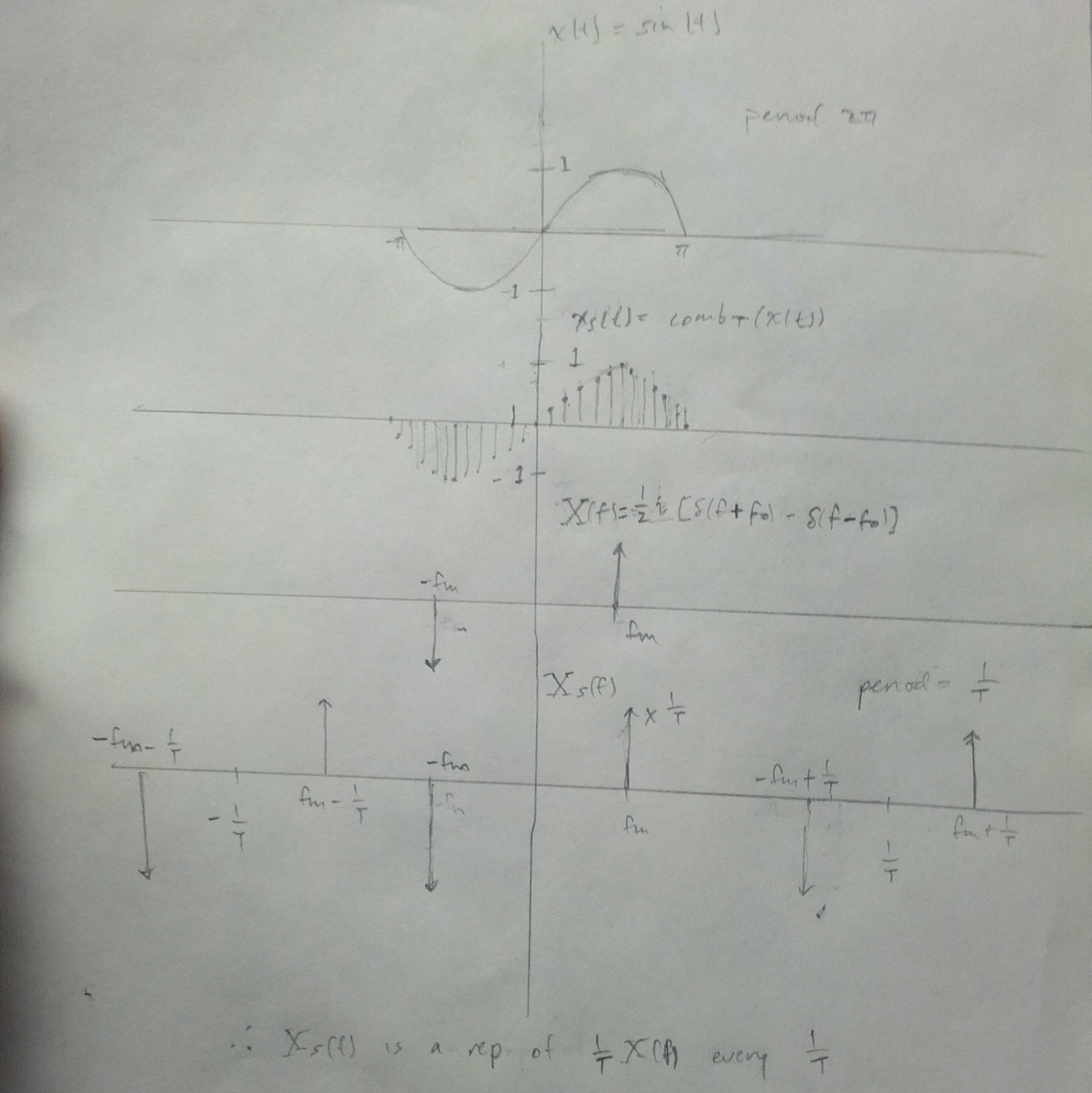
$ \begin{align} comb_T(x(t)) &= x(t) \times p_T(t) &= x_s(t)\\ \end{align} $ The comb of a signal is equal to the signal multiplied by an impulse train. $ \begin{align} X_s(f) &= F(x_s(t)) = F(comb_T(x(t))\\ &= F(x(t)p_T(t))\\ &= X(f) * F(p_T(f)\\ \end{align} $ Multiplication in time is equal to convolution in frequency.
$ \begin{align} X_s(f)&= X(f)*\frac{1}{T}\sum_{n = -\infty}^\infty \delta(f-\frac{n}{T})\\ &= \frac{1}{T}X(f)*p_\frac{1}{T}(f)\\ &= \frac{1}{T}rep_\frac{1}{T}X(f)\\ \end{align} $ The result is a repetition of the fourier transformed signal.
Conclusion
Xs(f) is a rep of X(f) in the frequency domain with amplitude of 1/T and period of 1/T.