| Line 18: | Line 18: | ||
''MATLAB Plot of <math>X_{s}</math>(f)'' | ''MATLAB Plot of <math>X_{s}</math>(f)'' | ||
| + | |||
| + | [[Image:stein_test_picture.png]] | ||
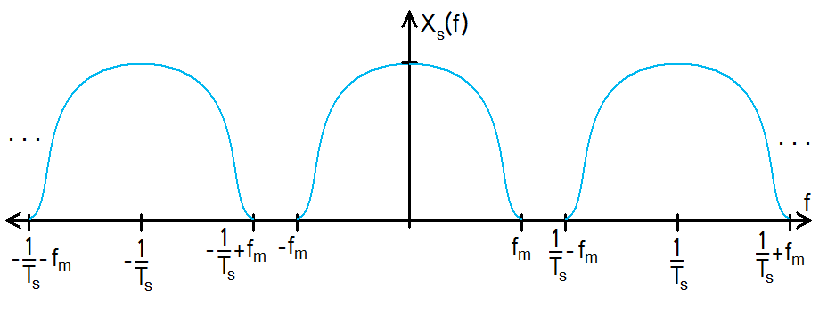
Observe that <math>X_{s}</math>(f) consists of <math>(1/T_{s})</math>*X(f) repeated every <math>1/T_{s}</math>. | Observe that <math>X_{s}</math>(f) consists of <math>(1/T_{s})</math>*X(f) repeated every <math>1/T_{s}</math>. | ||
Revision as of 13:42, 4 October 2014
Slecture_Nyquist_Theorem_Stein
The Nyquist Theorem states that it is possible to reproduce a signal from sampled version of that signal given that the sampling frequency is greater than twice the greatest frequency component of the original signal.
Proof
Let's begin by looking at X(f) and $ X_{s} $(f):
MATLAB Plot of X(f)
MATLAB Plot of $ X_{s} $(f)
Observe that $ X_{s} $(f) consists of $ (1/T_{s}) $*X(f) repeated every $ 1/T_{s} $.
If we use a low-pass filter with gain $ T_{s} $ on $ X_{s} $(f), we can obtain the original signal if the repetitions don't overlap.
For this case to be met, $ 1/T_{s} - f_{m} $ must be greater than $ f_{m} $.
In other words,
$ \frac{1}{T_{s}} > 2f_{m} $