| Line 64: | Line 64: | ||
https://www.projectrhea.org/rhea/images/4/4f/X1wplot.png | https://www.projectrhea.org/rhea/images/4/4f/X1wplot.png | ||
Repeats every <math>2\pi</math> | Repeats every <math>2\pi</math> | ||
| + | |||
| + | The frequency content of the original signal lies within the -<math>\pi</math> to <math>\pi </math> band. Therefore the signal can be properly reconstructed. | ||
<font size="4">Sampling <u>Below</u> Nyquist Frequency</font> | <font size="4">Sampling <u>Below</u> Nyquist Frequency</font> | ||
| Line 107: | Line 109: | ||
https://www.projectrhea.org/rhea/images/0/00/X2wplot.png | https://www.projectrhea.org/rhea/images/0/00/X2wplot.png | ||
| − | As you can see the original signal frequency exists outside of the <math> | + | As you can see the original signal frequency exists outside of the -<math>\pi</math> to <math>\pi </math> band. |
The frequencies that exists within this band are copies of the original signal that are 'rep'ed. Therefore these frequencies do not represent the frequency content of the the original signal, resulting in aliasing. | The frequencies that exists within this band are copies of the original signal that are 'rep'ed. Therefore these frequencies do not represent the frequency content of the the original signal, resulting in aliasing. | ||
Revision as of 19:11, 2 October 2014
DTFT of a Cosine Signal Sampled Above and Below the Nyquist Frequency
A slecture by ECE student Andrew Pawling
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
In this slecture we will look at an example that illustrates the Nyquist condition. When a signal is sampled, frequencies above half the sampling rate cannot be properly represented and result in aliasing.
Lets look at a pure tone frequency F4 = 349Hz
We will represent this tone as a cosine signal, $ cos*(2\pi349t) $
Sampling Above Nyquist Frequency
For this signal $ f_{s} > 2f_{m} = 2(349)Hz = 698Hz $ or else aliasing will occur. We will choose a sampling frequency of $ f_{s} = 1/T_{1} = 1000Hz $.
$ \begin{align} x_{1}(n) &= x(nT_{1}) \\ &= cos(2\pi349nT_{1}) \\ &= cos(\frac{2\pi349n}{1000}) \\ &= \frac{1}{2}(e^{\frac{-j2\pi349n}{1000}} + e^{\frac{j2\pi349n}{1000}}) \\ \\ \\ \end{align} $
$ Note\ that:\ 0 < |\pm2\pi\frac{349}{1000}| < \pi $
This means the original signal can be properly represented when sampled at $ f_{s} = 1000Hz. $
Using the discrete-time Fourier transform pair for cosine:
$ x[n] \ \ \ \ \ \ \ \ \ \ -----> \ \ \ \ X(\omega) $
$ cos(\omega_{0}n) \ \ \ \ -----> \ \ \ \ \pi\sum_{k=-\infty}^\infty (\delta(\omega -\omega_{0}+2\pi k) + \delta(\omega + \omega_{0}+2\pi k)) $
$ \begin{align} X_{1}(\omega) &= \pi \sum_{k=-\infty}^\infty(\delta(\omega - 2\pi\frac{349}{1000} +2\pi k) + \delta(\omega + 2\pi\frac{349}{1000} + 2\pi k)) \\ &= rep_{2\pi}\pi (\delta(\omega - 2\pi\frac{349}{1000}) + \delta(\omega + 2\pi\frac{349}{1000})) \\ \end{align} $
Plot of $ X_{1}(\omega) $:
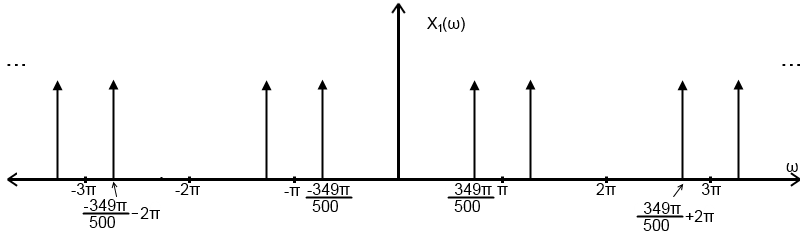 Repeats every $ 2\pi $
Repeats every $ 2\pi $
The frequency content of the original signal lies within the -$ \pi $ to $ \pi $ band. Therefore the signal can be properly reconstructed.
Sampling Below Nyquist Frequency
For this signal $ f_{s} > 2f_{m} = 2(349)Hz = 698Hz $ or else aliasing will occur. We will choose a sampling frequency that does not satisfy this condition this time. Let's use $ f_{s} = 1/T_{2} = 500Hz $.
$ \begin{align} x_{2}(n) &= x(nT_{2}) \\ &= cos(2\pi349nT_{2}) \\ &= cos(\frac{2\pi349n}{500}) \\ &= \frac{1}{2}(e^{\frac{-j2\pi349n}{500}} + e^{\frac{j2\pi349n}{500}}) \\ \\ \\ \end{align} $
$ Note\ that:\ \pi < |\pm2\pi\frac{349}{500}| < 2\pi $
This means the original signal cannot be properly represented when sampled at $ f_{s} = 500Hz. $
Using the discrete-time Fourier transform pair for cosine again:
$ x[n] \ \ \ \ \ \ \ \ \ \ -----> \ \ \ \ X(\omega) $
$ cos(\omega_{0}n) \ \ \ \ -----> \ \ \ \ \pi\sum_{k=-\infty}^\infty (\delta(\omega -\omega_{0}+2\pi k) + \delta(\omega + \omega_{0}+2\pi k)) $
$ \begin{align} X_{1}(\omega) &= \pi \sum_{k=-\infty}^\infty(\delta(\omega - 2\pi\frac{349}{500} +2\pi k) + \delta(\omega + 2\pi\frac{349}{500} + 2\pi k)) \\ &= rep_{2\pi}\pi (\delta(\omega - 2\pi\frac{349}{500}) + \delta(\omega + 2\pi\frac{349}{500})) \\ \end{align} $
Plot of $ X_{2}(\omega) $:
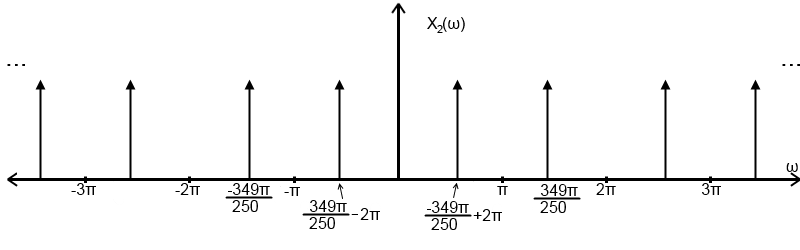
As you can see the original signal frequency exists outside of the -$ \pi $ to $ \pi $ band. The frequencies that exists within this band are copies of the original signal that are 'rep'ed. Therefore these frequencies do not represent the frequency content of the the original signal, resulting in aliasing.

