| Line 38: | Line 38: | ||
== DTFT of a Cosine Sampled Above the Nyquist Rate == | == DTFT of a Cosine Sampled Above the Nyquist Rate == | ||
| − | For our original pure frequency, let’s choose the E below middle C. The E occurs at 330''Hz'' <math>x(t) = cos(2π * 330t)</math> <p>Now let’s sample this pure cosine at a frequency above the Nyquist Rate. The Nyquist Rate is: <br><span class="math"> ''f''<sub>''s''</sub> = 2 * ''f''<sub>''m''''a''''x''</sub> = 2 * (330''H''''z'') = 660'' | + | For our original pure frequency, let’s choose the E below middle C. The E occurs at 330''Hz'' <math>x(t) = cos(2π * 330t)</math> <p>Now let’s sample this pure cosine at a frequency above the Nyquist Rate. The Nyquist Rate is: <br><span class="math"> ''f''<sub>''s''</sub> = 2 * ''f''<sub>''m''''a''''x''</sub> = 2 * (330''H''''z'') = 660''Hz''</span>. <br>Let’s sample at 990<span class="math">''Hz''</span>. |
<math> \begin{align} \\ | <math> \begin{align} \\ | ||
x_d[n] & = x(n*\frac{1}{990Hz})\\ | x_d[n] & = x(n*\frac{1}{990Hz})\\ | ||
| − | & = cos(2\pi n *\frac{330}{990}) = \frac{e^{j2\pi n \frac{330}{ | + | & = cos(2\pi n *\frac{330}{990}) = \frac{e^{j2\pi n \frac{330}{990}} + e^{-j2\pi n \frac{330}{990}}}{2}\\ |
& = cos(\frac{2\pi n}{3}) | & = cos(\frac{2\pi n}{3}) | ||
\end{align} | \end{align} | ||
| Line 59: | Line 59: | ||
== DTFT Of a Cosine Sampled Below the Nyquist Rate == | == DTFT Of a Cosine Sampled Below the Nyquist Rate == | ||
| − | <p>Let’s use the same pure frequency as above. | + | <p>Let’s use the same pure frequency as above.</p> |
| − | <p | + | <p><span class="math"><em>x</em>(<em>t</em>) = <em>c</em><em>o</em><em>s</em>(2<em>π</em> * 330<em>t</em>)</span><br /></p> |
<p>Now let’s sample this pure cosine at a frequency below the Nyquist Rate. From above, the Nyquist Rate is 660<span class="math"><em>H</em><em>z</em></span>. Let’s sample at 550<span class="math"><em>H</em><em>z</em></span>.</p> | <p>Now let’s sample this pure cosine at a frequency below the Nyquist Rate. From above, the Nyquist Rate is 660<span class="math"><em>H</em><em>z</em></span>. Let’s sample at 550<span class="math"><em>H</em><em>z</em></span>.</p> | ||
| − | <p><br />< | + | <p><br /> |
| − | + | ||
| − | + | <math> \begin{align} \\ | |
| − | \end{ | + | x_d[n] & = x(n*\frac{1}{550Hz})\\ |
| + | & = cos(2\pi n *\frac{330}{550}) = \frac{e^{j2\pi n \frac{330}{550}} + e^{-j2\pi n \frac{330}{550}}}{2}\\ \\ | ||
| + | \end{align} | ||
| + | </math> <br /><br /> | ||
| + | |||
| + | Because <font style="vertical-align:-125%;"><math>\pi < \frac{2\pi 330}{550} < 2\pi</math></font>, aliasing occurs in the DTFT. The DTFT should be calculated with <font style="vertical-align:-80%;"><math>\omega \in [-\pi,\pi]</math></font>, so we will use the periodicity of cosine to shift <math>x_d[n]</math> into an appropriate range. | ||
| + | |||
| + | <br /></p> | ||
<p><br /></p> | <p><br /></p> | ||
<p>Because <span class="math">$ \pi < \frac{2\pi 330}{550} < 2\pi$</span>, aliasing occurring in the DTFT. The DTFT should be calculated with <span class="math"><em>ω</em> ∈ [ − <em>π</em>, <em>π</em>]</span>, so we will use the periodicity of cosine to shift <span class="math"><em>x</em><sub><em>d</em></sub>[<em>n</em>]</span> into an appropriate range.</p> | <p>Because <span class="math">$ \pi < \frac{2\pi 330}{550} < 2\pi$</span>, aliasing occurring in the DTFT. The DTFT should be calculated with <span class="math"><em>ω</em> ∈ [ − <em>π</em>, <em>π</em>]</span>, so we will use the periodicity of cosine to shift <span class="math"><em>x</em><sub><em>d</em></sub>[<em>n</em>]</span> into an appropriate range.</p> | ||
| − | <p><br />< | + | <p><br / |
| − | x_{d}[n] & | + | ><math> \begin{align}\\ |
| − | & | + | x_{d}[n] & = cos(2\pi n*\frac{330}{550})\\ |
| − | & | + | & = cos(2\pi n*\frac{330}{550} - 2\pi n)\\ |
| − | & | + | & = cos(2\pi n*(\frac{330}{550} - \frac{550}{550}))\\ |
| − | & | + | & = cos(2\pi n*(\frac{-220}{550}))\\ |
| − | \end{ | + | & = cos(2\pi n*\frac{220Hz}{550Hz}) |
| + | \end{align} | ||
| + | </math><br /></p> | ||
<p>Now that <span class="math">$\ |2\pi\frac{220}{550}| < \pi$</span>, we can take the DTFT of <span class="math"><em>x</em><sub><em>d</em></sub>[<em>n</em>]</span>, and the initial value will fall into a desired range for <span class="math"><em>ω</em></span>.</p> | <p>Now that <span class="math">$\ |2\pi\frac{220}{550}| < \pi$</span>, we can take the DTFT of <span class="math"><em>x</em><sub><em>d</em></sub>[<em>n</em>]</span>, and the initial value will fall into a desired range for <span class="math"><em>ω</em></span>.</p> | ||
<p><br /><span class="math">$$\begin{split} | <p><br /><span class="math">$$\begin{split} | ||
Revision as of 10:12, 2 October 2014
DTFT of a Cosine Sampled Above and Below the Nyquist Rate
A slecture by ECE student Sahil Sanghani
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
Contents
Outline
- Introduction
- Useful Background
- DTFT Example of a Cosine Sampled Above the Nyquist Rate
- DTFT Example of a Cosine Sampled Below the Nyquist Rate
- Conclusion
- References
Introduction
In this Slecture, I will walk you through taking the DTFT of a pure frequency sampled above and below the Nyquist Rate. Then I will compare the differences between them.
Useful Background
Nyquist Condition: $ f_s = 2f_{max} $</font> DTFT of a Cosine: $ x_d[n] = cos(2\pi nT){\leftrightarrow}X(\omega) = \pi(\delta(\omega-\omega_o) + \delta(\omega+\omega_o)){ ,for\ } \omega \in [-\pi,\pi] $
The DTFT of a sampled signal is periodic with 2π.
DTFT of a Cosine Sampled Above the Nyquist Rate
For our original pure frequency, let’s choose the E below middle C. The E occurs at 330Hz $ x(t) = cos(2π * 330t) $ <p>Now let’s sample this pure cosine at a frequency above the Nyquist Rate. The Nyquist Rate is:
fs = 2 * fm'a'x = 2 * (330H'z) = 660Hz.
Let’s sample at 990Hz.
$ \begin{align} \\ x_d[n] & = x(n*\frac{1}{990Hz})\\ & = cos(2\pi n *\frac{330}{990}) = \frac{e^{j2\pi n \frac{330}{990}} + e^{-j2\pi n \frac{330}{990}}}{2}\\ & = cos(\frac{2\pi n}{3}) \end{align} $
Because $ \left | \frac{2\pi}{3}\right | < \pi $, there is no aliasing occurring in the DTFT, and it can be written as follows:
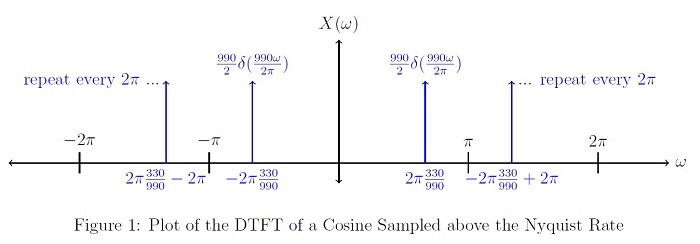
$ \begin{align} \\ X(\omega) & = \frac{1}{2}(2\pi\delta(\omega - 2\pi \frac{330}{990}) + 2\pi\delta(\omega + 2\pi \frac{330}{990})) , \ \omega \in\ [-\pi,\pi]\\ & = \frac{990}{2}(\delta(\frac{990}{2\pi}\omega - 330) + \delta(\frac{990}{2\pi}\omega + 330)) , \ \omega \in\ [-\pi,\pi]\\ & = rep_{2\pi}(\frac{990}{2}(\delta(\frac{990}{2\pi}\omega - 330) + \delta(\frac{990}{2\pi}\omega + 330))), \forall \omega \end{align} $
DTFT Of a Cosine Sampled Below the Nyquist Rate
Let’s use the same pure frequency as above.
x(t) = cos(2π * 330t)
Now let’s sample this pure cosine at a frequency below the Nyquist Rate. From above, the Nyquist Rate is 660Hz. Let’s sample at 550Hz.
$ \begin{align} \\ x_d[n] & = x(n*\frac{1}{550Hz})\\ & = cos(2\pi n *\frac{330}{550}) = \frac{e^{j2\pi n \frac{330}{550}} + e^{-j2\pi n \frac{330}{550}}}{2}\\ \\ \end{align} $
Because $ \pi < \frac{2\pi 330}{550} < 2\pi $, aliasing occurs in the DTFT. The DTFT should be calculated with $ \omega \in [-\pi,\pi] $, so we will use the periodicity of cosine to shift $ x_d[n] $ into an appropriate range.
Because $ \pi < \frac{2\pi 330}{550} < 2\pi$, aliasing occurring in the DTFT. The DTFT should be calculated with ω ∈ [ − π, π], so we will use the periodicity of cosine to shift xd[n] into an appropriate range.
$ \begin{align}\\ x_{d}[n] & = cos(2\pi n*\frac{330}{550})\\ & = cos(2\pi n*\frac{330}{550} - 2\pi n)\\ & = cos(2\pi n*(\frac{330}{550} - \frac{550}{550}))\\ & = cos(2\pi n*(\frac{-220}{550}))\\ & = cos(2\pi n*\frac{220Hz}{550Hz}) \end{align} $
Now that $\ |2\pi\frac{220}{550}| < \pi$, we can take the DTFT of xd[n], and the initial value will fall into a desired range for ω.
$$\begin{split}
X(\omega) & = \frac{1}{2}(2\pi\delta(\omega - 2\pi \frac{220}{550}) + 2\pi\delta(\omega + 2\pi \frac{220}{550})) , \ \omega \in\ [-\pi,\pi]\\
& = \frac{550}{2}(\delta(\frac{550}{2\pi}\omega - 220) + \delta(\frac{550}{2\pi}\omega + 220)) , \ \omega \in\ [-\pi,\pi]\\
& = rep_{2\pi}(\frac{550}{2}(\delta(\frac{550}{2\pi}\omega - 220) + \delta(\frac{550}{2\pi}\omega + 220))), \forall \omega
\end{split}$$