| Line 20: | Line 20: | ||
According to Euler Characteristic, any convex polyhedron's surface has Euler characteristic E+2=V+F.<br> | According to Euler Characteristic, any convex polyhedron's surface has Euler characteristic E+2=V+F.<br> | ||
Note that Polyhedral is composed of multiple faces. <br><br> | Note that Polyhedral is composed of multiple faces. <br><br> | ||
| − | |||
Remove one face of the polyhedral surface and Pulled the edges of the missing face away from each other, deform all the rest into a planar graph of points and curves(Assuming that polyhedral surface is homeomorphic to the sphere). After this deformation, the regular faces are generally not regular anymore. The number of vertices and edges has remained the same, but the number of faces has been reduced by 1. Therefore, proving Euler's formula for the polyhedron reduces to proving V − E + F =1 for this deformed, planar object.<br><br> | Remove one face of the polyhedral surface and Pulled the edges of the missing face away from each other, deform all the rest into a planar graph of points and curves(Assuming that polyhedral surface is homeomorphic to the sphere). After this deformation, the regular faces are generally not regular anymore. The number of vertices and edges has remained the same, but the number of faces has been reduced by 1. Therefore, proving Euler's formula for the polyhedron reduces to proving V − E + F =1 for this deformed, planar object.<br><br> | ||
Apply repeatedly either of the following two transformations, maintaining the invariant that the exterior boundary is always a simple cycle:<br><br> | Apply repeatedly either of the following two transformations, maintaining the invariant that the exterior boundary is always a simple cycle:<br><br> | ||
| Line 48: | Line 47: | ||
<br> | <br> | ||
<br> | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | Resources:<br> | ||
| + | •Refer to Wiki Euler characteristic:<br><br> | ||
| + | http://en.wikipedia.org/wiki/Euler_characteristic<br> | ||
<br> | <br> | ||
<br> | <br> | ||
Revision as of 10:11, 27 April 2014
Simplicial complexes: higher dimensional versions of graphs
Prepared by: Weijie Huo(huow@purdue.edu)
April 26, 2014
1.The idea to points that can also be grouped into triangles, or tetrahedra:
Grouped into triangles:
•By the definition of triangulation. For the graph which has been grouped into triangles, it has the following property. None of the edge intersect more than 3 points. None of the edge intersect with other edges.
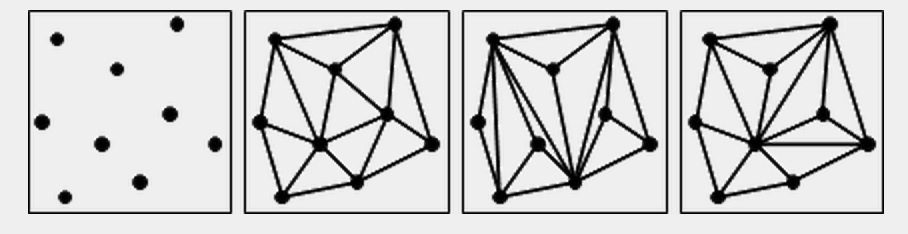
Grouped into tetrahedra:
•By the definition, In 3D, for the graph which has been grouped into tetrahedra, it has the following property. None of the tetrahedra intersect more than 4 points. None of the tetrahedra intersect with other tetrahedra.
2.Geometric meaning of Euler’s formula, E+2=V+F:
According to Euler Characteristic, any convex polyhedron's surface has Euler characteristic E+2=V+F.
Note that Polyhedral is composed of multiple faces.
Remove one face of the polyhedral surface and Pulled the edges of the missing face away from each other, deform all the rest into a planar graph of points and curves(Assuming that polyhedral surface is homeomorphic to the sphere). After this deformation, the regular faces are generally not regular anymore. The number of vertices and edges has remained the same, but the number of faces has been reduced by 1. Therefore, proving Euler's formula for the polyhedron reduces to proving V − E + F =1 for this deformed, planar object.
Apply repeatedly either of the following two transformations, maintaining the invariant that the exterior boundary is always a simple cycle:
1.Remove a triangle with only one edge adjacent to the exterior, as illustrated by the second graph. This decreases the number of edges and faces by one each and does not change the number of vertices, so it preserves V − E + F.
2.Remove a triangle with two edges shared by the exterior of the network, as illustrated by the third graph. Each triangle removal removes a vertex, two edges and one face, so it preserves V − E + F.
Remove a triangle with two edges shared by the exterior of the network, as illustrated by the third graph. Each triangle removal removes a vertex, two edges and one face, so it preserves V − E + F.
These transformations eventually reduce the planar graph to a single triangle. (Without the simple-cycle invariant, removing a triangle might disconnect the remaining triangles, invalidating the rest of the argument. A valid removal order is an elementary example of a shelling.)
At this point the lone triangle has V = 3, E = 3, and F = 1, so that V − E + F = 1. Since each of the two above transformation steps preserved this quantity, we have shown V − E + F = 1 for the deformed, planar object thus demonstrating V − E + F = 2 for the polyhedron. This proves the theorem.
•Let me use one example to illustrate my understanding of Euler characteristic:
Use Convex Hull Algorithm to find the convex out layer of the graph
In the first graph below, there are total n points in the graph and there are h points founded by the convex hull algorithm which form the polygon and k which are inside the polygon(Note: h + k = n). Obviously, for those h points, it can be divided into h-2 triangles as second graph shown below. Traverse k points one by one and Connect them with those 3 points that form the out-triangle(the closest one, it can be done by calling the function recursively until all k points are traversed). Once “out-triangle”s points are connected to one of the k points, it can no longer form the triangle, but inside the “out-triangle”, there are three “in-triangles” are formed ==> for each k point being traversed, it generate 2 more triangles. ==> There are (h-2) + 2*k triangles are formed by triangulation Algorithm.
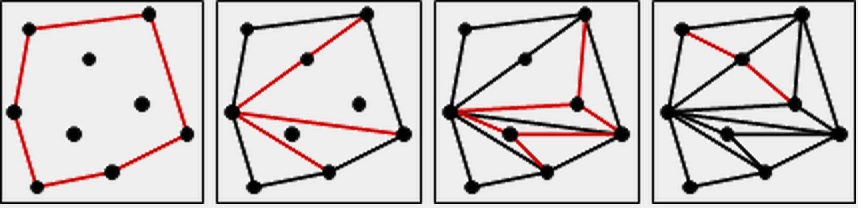
On the other hand, we know that convex hull contains h-1 edges and for each k points, it “generates” 3 edges. ==> The edges of the triangulation graph is h - 1 + h - 3 + 3 * k = (2h - 4) + 3*k
According to the result calculated above.
1.There are (h-2) + 2*k triangles are formed by triangulation Algorithm.
2.The edges of the triangulation graph is h - 1 + h - 3 + 3 * k = (2h - 4) + 3*k
E = (2h - 4) + 3*k; V = h + k; F = number of triangles = (h-2) + 2*k triangles;
Obviously, (2h - 4) + 3*k + 2 = h + k + (h-2) + 2*k ====>> E + 2 = V + F
3.what might replace this formula compare a "triangulated" sphere to a "triangulated" doughnut:
If the surface of a polyhedron have h(h>=0, the number of tori in a connected sum decomposition of the surface/number of handles) then the Euler characteristic is 2 - 2*h ==> E + 2 - 2*h = V + F
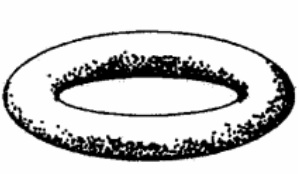
We know that the number of handle of "triangulated" doughnut is 1. According to the equation above ==> E + 2- 2*1 = V + F ==> E = V + F
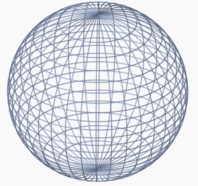
The number of handles of "triangulated" sphere is 1. According to the equation above ==> E + 2- 2*0 = V + F ==> E + 2 = V + F
Resources:
•Refer to Wiki Euler characteristic:
http://en.wikipedia.org/wiki/Euler_characteristic
Back to MA375 Spring 2014

