Revision as of 23:51, 30 November 2013

Mark Rosinski, markrosi@purdue.edu Joseph Lam, lam5@purdue.edu Beichen Xiao, xiaob@purdue.edu

In this project, we would like to introduce some basic information about P-groups and Sylow Theorem.

P-groups

Definitions:

• Let p be a prime p be an integer greater or equal to 0. A p-group is a group of order pⁿ.
• A subgroup of order p^k for some k ≥ 1 is called a p-subgroup.
• If |G| = p^αm where p does not divide m, then a subgroup of order p^α is called a Sylow p-subgroup of G.

Propositions:

If G is a p-group then G contains an element of order p.

1. If G is a p-group then Z(G)cannot be equal to {1}
2. Let p be a prime and let G be a group of order p². Then G is abelian.
3. If G is a p-group of order pa, then there exists a chain, {1} is contained in N1 contained in N2 contained in...contained in Na-1 contained in Gof normal subgroups of G, such that |Ni|=pi.

All content above and proofs of these Propositions can be found here

Further Information on p-groups:

• Lie Algebras
  • A lie ring is a set R with two binary operations - addition and the Lie bracket - such that
    • (R,+) is an abelian group;
    • Bilinearity: The bracket operation distributes over addition;
    • Alternating on the vector space g: [x,x] = 0 for all x in R;
    • The Jacobi Identity: [[x,y],z]+[[y,z],x]+[[z,x],y]=0 for all x,y,z in R.
  • If F is a field, and R is an F-vector space with a[x,y]=[ax,y] then R is a Lie algebra.
  • To every finite p-group one can associate a Lie ring L(G), and if G/G' is abelian then L(G) is actually a lie algebra over the finite field GF(p).
    • Proposition: Let φ be an automorphism of the finite p-group G. Then φ induces an automorphism on L(G), and if φ has order prime to p, then the induced automorphism has the same order.

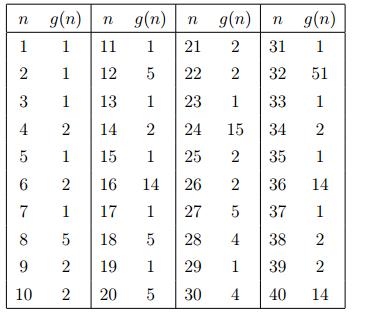
• Number of Groups
  • Let g(n) denote the number of groups of order n.
    • i) g(p)=1 for p a prime.
    • ii) if p<q, then g(pq)=1 if q is not congruent to 1 mod p, and g(pq)=2 otherwise.
    • iii) g(p²)=2.
    • iv) g(p³)=5.

From this we can see that the number of groups of order n depends more on the prime structure then on its size.

Look at this table to help explain this notion:

All content of Lie Algebras and Number of groups from this page can be found from here as well as additional information on these topics. 

Automorphism Groups of order pⁿ

Propositions:

1. Let G denote the elementary abelian group of order pⁿ.  Then $ Aut(G)\cong GL_{n}(p) $, the group of n x n matrices over GF(p). 
2. Let G denote the cyclic group of order n.  Then Aut(G) is abeilan, and has order φ(n), where φ denotes Euler's φ-fuction.
3. Let G be a cyclic p-group with p odd, and write A=Aut(G). Then A is cyclic.

All information from this section is available from here as well as further information and proofs of these propositions on Automorphism Groups of order pⁿ. 

Classification of p-groups

1. Regular p-groups

• Definitions:

• • For every $ a, b \in G $ there exist $ c \in [<a,b>,<a,b>] $ such that a^p b^p = (ab)^p c^p
  • For every $ a, b \in G $ there exist $ c_i \in [<a,b>,<a,b>] $ such that $ a^p b^p = (ab)^p c^p _1 c^p _2 . . . c^p _i $
  • For evert $ a, b \in G $ and every positive integer n there exist elements $ c_i \in [<a,b>,<a,b>] $ such that $ a^q b^q = (ab)^q c^q _1 c^q _2 . . . c^q _i $ where $ q = p^n $

2. Powerful p-groups

• Definition:

• • $ G $ is powerful if $ \mho _1 (G) \supseteq G' $
  • Let $ N \triangleleft G $, then $ N $ is powerfully embedded in $ G $ if $ \mho _1 (N) \supseteq [N,G] $. $ G $ is powerful IFF it is powerfully embedded in itself. If $ N $ is powerfully embedded in $ G $, then $ N $ is powerful, more importantly, if $ N \subseteq H \subseteq G $ and $ H \div N $ is cyclic, then $ \mho _1 (H) \supseteq \mho _1 (N) \supseteq [N,H] = H' $, so H is powerful

• Proposition:
  • G is powerful IFF G is powerfully embedded in G
  • If N is powerfully embedded in G, then N is powerful and G centralizes $ N \div N^p $
  • If $ K \triangleleft G $ and $ N $ is powerfully embedded in G then $ (N \times K) \div K $ is powerfully embedded in $ G \div K $
  • If N is powerfully embedded in G and $ x \in G $ then $ <x>N $ is powerful
  • If M is powerfully embedded in G and N is powerfully embedded in G, then $ (M \times N) $ is powerfully embedded in G

All information from this section is available from [here] as well as further information and proofs on Powerful p-groups

NOTE TO GROUP7

I found Pro p-groups to be irreverent because I feel it is a small part of p-groups. But, if you think there is a need for Pro p-groups, let me know.

Sylow's Theorems

Who is Sylow?

Peter Ludwig Mejdell Sylow (12 December 1832 – 7 September 1918) was a Norwegian mathematician who proved foundational results in group theory. He was born and died in Christiania (now Oslo).

Sylow was a high school teacher in Halden, Norway, from 1858 to 1898, and a substitute lecturer at Christiania University in 1862, covering Galois theory. It was then that he posed the question that led to his theorems regarding Sylow subgroups. Sylow published the Sylow theorems in 1872, and subsequently devoted eight years of his life, with Sophus Lie, to the project of editing the mathematical works of his countryman, Niels Henrik Abel.

He was appointed professor of Christiania University in 1898.

Notation:

Syl_p(G) = the set of Sylow p-subgroups of G

n_p(G)= the # of Sylow p-subgroups of G =|Syl_p(G)|

Theorems:

Let G be a group of order p^αm, where p is a prime, m≥1, and p does not divide m.  Then:

1. Syl_p(G) cannot be the empty set. 
2. All Sylow p-subgroups are conjugate in G. To expand, if P₁ and P₂ are both Sylow p-subgroups, then there is some g in G such that P₁=gP₁g^-1.                           In particular, n_p(G)=(G:N_G(P)).
3. Any p-subgroup of G is contained in a Sylow p-subgroup
4. n_p(G) is congruent to 1 mod p. 

All content from this section and proofs of these Theorems can be found here

Application of Sylow theorems:

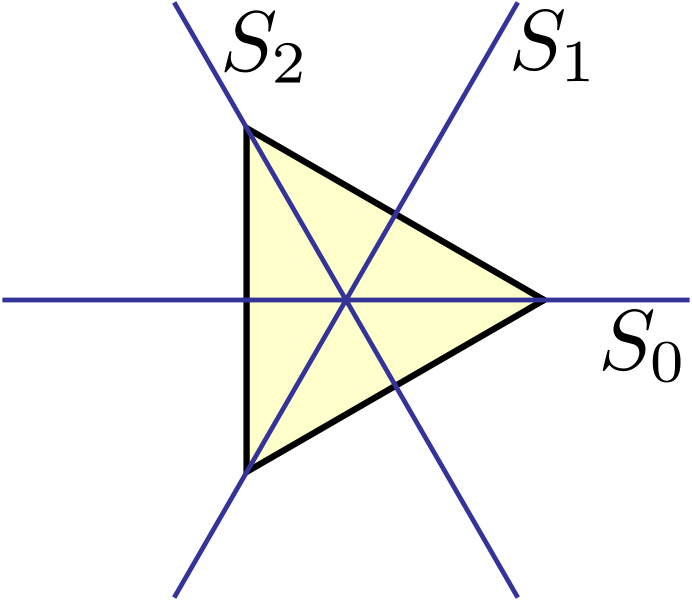
• In D₆ all reflections are conjugate, as reflections correspond to Sylow 2-subgroups.

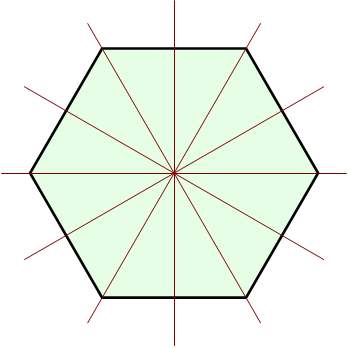
• In D₁₂ reflections no longer correspond to Sylow 2-subgroups, and fall into two conjugacy classes.

Extra Information

For students looking for extensive history on p-groups, Sylow's Theorems and finite simple groups in general you can find this information here

References

Sikimeti Ma'u. Notes on Sylow's Theorems. Retrieved from math.berkeley.edu/~sikimeti/SylowNotes.pdf

Alavaro Loustau. Latex Tutorial.  Retrieved from omega.albany.edu:8008/Symbols.html

David A. Craven. The Theory of p-Groups. Retrieved from [http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf&nbsp;

Ronald Solomon.  A Brief History of the Classification of the Finite Simple Groups www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf
http://groupprops.subwiki.org/wiki/Regular_p-group (I'm not confident we should use this as a reference.  It's like usign wikipedia, very frowned upon.)

Marshall Hall, "The Theory of Groups." Retrieved from [here]

Alexander Lubotzky. "Powerful p-Groups. I. Finite Groups." Retrieved from [here]

Bruno Kahn. "A Characterization of Powerfully Embedded Normal Subgroups of a p-Group." Retrieved from [here]

Charles Richard Leedham-Green. "The Structure of Groups of Prime Power Order." Retrieved from [here]

I saw other groups' references and they use wikipedia as a reference so i just write them down. Please feel free to erase them if you guys think it is not necessary.

Retrieved from [1]

Retrieved from [2]