| Line 3: | Line 3: | ||
Outline: | Outline: | ||
| − | + | <br> | |
= Email the group to see if anyone else is currently making changes before you begin making changes yourself!!!<br> = | = Email the group to see if anyone else is currently making changes before you begin making changes yourself!!!<br> = | ||
| Line 43: | Line 43: | ||
***Proposition: Let <span class="texhtml">φ</span> be an automorphism of the finite p-group G. Then <span class="texhtml">φ</span> induces an automorphism on L(G), and if <span class="texhtml">φ</span> has order prime to p, then the induced automorphism has the same order. | ***Proposition: Let <span class="texhtml">φ</span> be an automorphism of the finite p-group G. Then <span class="texhtml">φ</span> induces an automorphism on L(G), and if <span class="texhtml">φ</span> has order prime to p, then the induced automorphism has the same order. | ||
| − | + | <br> | |
*Number of Groups | *Number of Groups | ||
| Line 49: | Line 49: | ||
***i) g(p)=1 for p a prime. | ***i) g(p)=1 for p a prime. | ||
***ii) if p<q, then g(pq)=1 if q is not congruent to 1 mod p, and g(pq)=2 otherwise. | ***ii) if p<q, then g(pq)=1 if q is not congruent to 1 mod p, and g(pq)=2 otherwise. | ||
| − | ***iii) g( | + | ***iii) g(p<sup>2</sup>)=2. |
| − | ***iv) g( | + | ***iv) g(p<sup>3</sup>)=5. |
From this we can see that the number of groups of order n depends more on the prime structure then on its size. | From this we can see that the number of groups of order n depends more on the prime structure then on its size. | ||
| Line 56: | Line 56: | ||
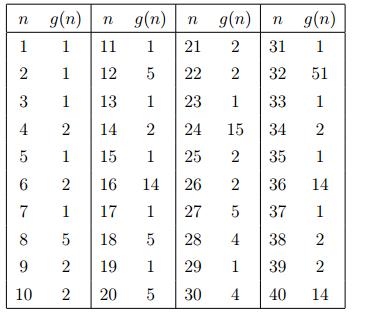
Look at this table to help explain this notion: | Look at this table to help explain this notion: | ||
| − | [[Image: | + | [[Image:N groups.jpg]] |
| − | All content of Lie Algebras and Number of groups from this page can be found from [http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf here] as well as additional information on these topics. | + | All content of Lie Algebras and Number of groups from this page can be found from [http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf here] as well as additional information on these topics. |
| + | |||
| + | == <br>Automorphism Groups of order p<sup>n</sup> == | ||
| + | |||
| + | '''Propositions:''' | ||
| + | |||
| + | #Let G denote the elementary abelian group of order p<sup>n</sup>. Then <math>Aut(G)\cong GL_{n}(p)</math>, the group of n x n matrices over GF(p). | ||
| + | #Let G denote the cyclic group of order n. Then Aut(G) is abeilan, and has order <span class="texhtml">φ</span>(n), where <span class="texhtml">φ </span>denotes Euler's <span class="texhtml">φ</span>-fuction. | ||
| + | #Let G be a cyclic p-group with p odd, and write A=Aut(G). Then A is cyclic. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | All information from this section is available from [http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf here] as well as further information and proofs of these propositions on Automorphism Groups of order p<sup>n</sup>. | ||
| − | |||
| − | |||
== Regular p-groups == | == Regular p-groups == | ||
| Line 105: | Line 115: | ||
For students looking for extensive history on p-groups, Sylow's Theorems and finite simple groups in general you can find this information [http://www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf here] | For students looking for extensive history on p-groups, Sylow's Theorems and finite simple groups in general you can find this information [http://www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf here] | ||
| + | <br> | ||
| + | == References == | ||
| − | + | I've been using these websites: <br>http://math.berkeley.edu/~sikimeti/SylowNotes.pdf<br>http://omega.albany.edu:8008/Symbols.html (this is Tex symbols)<br>http://www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf<br>and also the pdf emailed to you<br>http://groupprops.subwiki.org/wiki/Regular_p-group regular p-group<br>http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf this one is almost about everything. | |
| − | + | ||
| − | I've been using these websites: <br>http://math.berkeley.edu/~sikimeti/SylowNotes.pdf<br>http://omega.albany.edu:8008/Symbols.html (this is Tex symbols)<br>http://www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf<br>and also the pdf emailed to you<br>http://groupprops.subwiki.org/wiki/Regular_p-group regular p-group<br>http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf this one is almost about everything. | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
[[Category:MA453Fall2013Walther]] | [[Category:MA453Fall2013Walther]] | ||
Revision as of 12:35, 30 November 2013
Mark Rosinski, markrosi@purdue.edu Joseph Lam, lam5@purdue.edu Beichen Xiao, xiaob@purdue.edu
Outline:
Contents
Email the group to see if anyone else is currently making changes before you begin making changes yourself!!!
P-groups
Definitions:
- Let p be a prime p be an integer greater or equal to 0. A p-group is a group of order pn.
- A subgroup of order pk for some k ≥ 1 is called a p-subgroup.
- If |G| = pαm where p does not divide m, then a subgroup of order pα is called a Sylow p-subgroup of G.
Propositions:
If G is a p-group then G contains an element of order p.
- If G is a p-group then Z(G)cannot be equal to {1}
- Let p be a prime and let G be a group of order p2. Then G is abelian.
- If G is a p-group of order pa, then there exists a chain, {1} is contained in N1 contained in N2 contained in...contained in Na-1 contained in Gof normal subgroups of G, such that |Ni|=pi.
All content above and proofs of these Propositions can be found here
Further Information on p-groups:
- Lie Algebras
- A lie ring is a set R with two binary operations - addition and the Lie bracket - such that
- (R,+) is an abelian group;
- Bilinearity: The bracket operation distributes over addition;
- Alternating on the vector space g: [x,x] = 0 for all x in R;
- The Jacobi Identity: [[x,y],z]+[[y,z],x]+[[z,x],y]=0 for all x,y,z in R.
- If F is a field, and R is an F-vector space with a[x,y]=[ax,y] then R is a Lie algebra.
- To every finite p-group one can associate a Lie ring L(G), and if G/G' is abelian then L(G) is actually a lie algebra over the finite field GF(p).
- Proposition: Let φ be an automorphism of the finite p-group G. Then φ induces an automorphism on L(G), and if φ has order prime to p, then the induced automorphism has the same order.
- A lie ring is a set R with two binary operations - addition and the Lie bracket - such that
- Number of Groups
- Let g(n) denote the number of groups of order n.
- i) g(p)=1 for p a prime.
- ii) if p<q, then g(pq)=1 if q is not congruent to 1 mod p, and g(pq)=2 otherwise.
- iii) g(p2)=2.
- iv) g(p3)=5.
- Let g(n) denote the number of groups of order n.
From this we can see that the number of groups of order n depends more on the prime structure then on its size.
Look at this table to help explain this notion:
All content of Lie Algebras and Number of groups from this page can be found from here as well as additional information on these topics.
Automorphism Groups of order pn
Propositions:
- Let G denote the elementary abelian group of order pn. Then $ Aut(G)\cong GL_{n}(p) $, the group of n x n matrices over GF(p).
- Let G denote the cyclic group of order n. Then Aut(G) is abeilan, and has order φ(n), where φ denotes Euler's φ-fuction.
- Let G be a cyclic p-group with p odd, and write A=Aut(G). Then A is cyclic.
All information from this section is available from here as well as further information and proofs of these propositions on Automorphism Groups of order pn.
Regular p-groups
Definitons:
- For every $ a, b \in G $ there exists $ c \in [<a,b>,<a,b>] $ such that apbp = (a'b)pcp
- For every $ a, b \in G $ there exist $ c_1 , c_2 , . . . , c_k \in [<a,b>,<a,b>] $ such that $ a^p b^p = (ab)^p c^p _1 c^p _2 . . . c^p _k $
- For evert $ a, b \in G $ and every natural number n there exist Failed to parse (syntax error): c_1 , c_2 , . . . , c_k \in {,a,b>,<a,b>]
such that $ a^q b^q = (ab)^q c^q _1 c^q _2 . . . c^q _k $ where q = pn
Sylow's Theorems
Notation:
Sylp(G) = the set of Sylow p-subgroups of G
np(G)= the # of Sylow p-subgroups of G =|Sylp(G)|
Theorems:
Let G be a group of order pαm, where p is a prime, m≥1, and p does not divide m. Then:
- Sylp(G) cannot be the empty set.
- All Sylow p-subgroups are conjugate in G. To expand, if P1 and P2 are both Sylow p-subgroups, then there is some g in G such that P1=gP1g-1. In particular, np(G)=(G:NG(P)).
- Any p-subgroup of G is contained in a Sylow p-subgroup
- np(G) is congruent to 1 mod p.
All content from this section and proofs of these Theorems can be found here
Extra Information
For students looking for extensive history on p-groups, Sylow's Theorems and finite simple groups in general you can find this information here
References
I've been using these websites:
http://math.berkeley.edu/~sikimeti/SylowNotes.pdf
http://omega.albany.edu:8008/Symbols.html (this is Tex symbols)
http://www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf
and also the pdf emailed to you
http://groupprops.subwiki.org/wiki/Regular_p-group regular p-group
http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf this one is almost about everything.