| Line 25: | Line 25: | ||
<br> | <br> | ||
'''Crystal Symmetries and their properties'''<br><hr><br> | '''Crystal Symmetries and their properties'''<br><hr><br> | ||
| − | Many important material properties depend on crystal structure. Some of <br> | + | Many important material properties depend on crystal structure. Some of these <br> |
| − | + | include the following inexhaustive list: conductivity, magnetism, stiffness, and<br> | |
| − | + | strength. <br> | |
| − | Miller Indices represent an efficient way to label the orientation <br> | + | Miller Indices represent an efficient way to label the orientation of the crystals.<br> |
| − | + | For planes, the Miller Index value is the reciprocal of the value of the <br> | |
| − | of the value of the intersection of the plane with a particular axis, | + | intersection of the plane with a particular axis, converted to whole numbers. For <br> |
| − | converted to whole numbers. For directions in a crystal lattice, the | + | directions in a crystal lattice, the index is the axis coordinate of the end point<br> |
| − | index is the axis coordinate of the end point of the vector, converted | + | of the vector, converted to the nearest whole number. <br> |
| − | to the nearest whole number. <br> | + | |
[[Image:Miller.PNG]] <br> | [[Image:Miller.PNG]] <br> | ||
Revision as of 06:13, 17 November 2013
Crystals and Symmetry
NamesJason Krupp (krupp@purdue.edu)
Erik Plesha (eplesha@purdue.edu)
Andrew Wightman (awightma@purdue.edu)
Thilagan Sekaran(trajasek@purdue.edu)
A) Crystal Symmetries and Their Properties
--Miller Indices
--Slip Systems
--Group Properties
B) Crystal Movement and Symmetry
--Translational Movement
--Rotational Movement
--Mirror Movement
C)Combinations of Symmetry Operations
--32 Crystal Classes
D)Crystal Symmetry Groups
--Finite Symmetry Groups
--Non-Finite Symmetry Groups
Many important material properties depend on crystal structure. Some of these
include the following inexhaustive list: conductivity, magnetism, stiffness, and
strength.
Miller Indices represent an efficient way to label the orientation of the crystals.
For planes, the Miller Index value is the reciprocal of the value of the
intersection of the plane with a particular axis, converted to whole numbers. For
directions in a crystal lattice, the index is the axis coordinate of the end point
of the vector, converted to the nearest whole number.
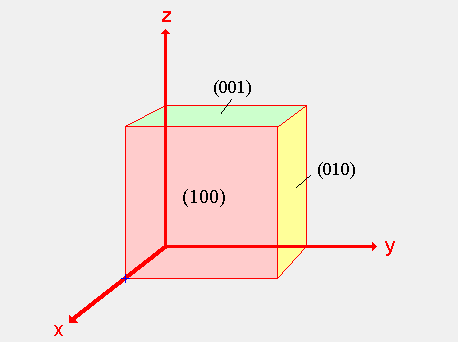
For example, the figure above depicts 3 of the 6 cube faces and the corresponding
Miller Indices. The red plane is labeled as (100) because the plane is shifted 1
unit in the x-direction. The yellow plane is labeled (010) because it is shifted 1
unit in the y-direction. Finally, the green plane is labeled (001) because it is
shifted 1 unit in the z-direction.
Combinations of Symmetry Operations
Crystal Symmetry Groups
References and Links
Gallian, J. (2013). Contemporary abstract algebra. (8th ed.). Boston, MA: Brooks/Cole, Cengage Learning.
MA 453 Notes