| Line 323: | Line 323: | ||
<td>=</td> | <td>=</td> | ||
<td></td> | <td></td> | ||
| − | <td><math>\begin{align} \frac{\pi_{k=0}^{3}(1+r_k)}{1+(r_0r_1+r_1r_2+r_2r_3)Z^{-1}+(r_0r_1r_2r_3+r_0r_2+r_1r_3)Z^{-2}+r_0r_3Z^{-3}}\\\end{align} </math></td> | + | <td><math>\begin{align} \frac{\pi_{k=0}^{3}(1+r_k)Z^{-3/2}}{1+(r_0r_1+r_1r_2+r_2r_3)Z^{-1}+(r_0r_1r_2r_3+r_0r_2+r_1r_3)Z^{-2}+r_0r_3Z^{-3}}\\\end{align} </math></td> |
</tr> | </tr> | ||
</table> | </table> | ||
Revision as of 15:25, 13 November 2013
Question 1
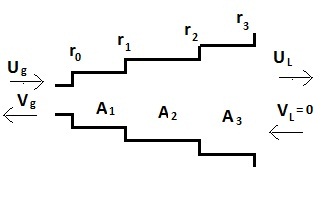
(a)
|
= | $ \begin{align} \frac{1}{1+r_0} \\\end{align} $ |
|
$ \begin{align} Z^{1/2} \\\end{align} $ |
|
$ \begin{align} \frac{1}{1+r_1} \\\end{align} $ |
|
$ \begin{align}Z^{1/2} \\\end{align} $ |
|
$ \begin{align} \frac{1}{1+r_2} \\\end{align} $ |
|
$ \begin{align}Z^{1/2} \\\end{align} $ |
|
$ \begin{align} \frac{1}{1+r_3} \\\end{align} $ |
|
|
| = | $ \begin{align} \frac{Z^{3/2}}{\pi_{k=0}^{3}(1+r_k)} \\\end{align} $ |
|
$ \begin{align} U_L \\\end{align} $ |
| = | $ \begin{align} \frac{Z^{3/2}}{\pi_{k=0}^{3}(1+r_k)} \\\end{align} $ |
|
$ \begin{align} U_L \\\end{align} $ |
| $ \begin{align} V(Z) \\\end{align} $ | = | $ \begin{align} \frac{U_L}{U_g} \\\end{align} $ | = | $ \begin{align} \frac{\pi_{k=0}^{3}(1+r_k)Z^{-3/2}}{1+(r_0r_1+r_1r_2+r_2r_3)Z^{-1}+(r_0r_1r_2r_3+r_0r_2+r_1r_3)Z^{-2}+r_0r_3Z^{-3}}\\\end{align} $ |
b) From the transfer function, we can see that there are three poles. If the poles are all real, there are three formants.
If one pole is real and the other are complex pole pair, there are two formants.
c) We can change the area of each segments. In this way,$ r_k $ will change , thus the root of the denominator of V(Z) is changed, which determines the location of formants.