| Line 203: | Line 203: | ||
Attach a copy of your lab record to the report. Answer any specific questions asked in the lab | Attach a copy of your lab record to the report. Answer any specific questions asked in the lab | ||
manual. | manual. | ||
| + | |||
| + | == VI. APPENDIX == | ||
| + | |||
| + | The logarithmic notation: Bels and decibels | ||
| + | |||
| + | The logarithmic notation provides an easy way to specify numbers and quantities that can | ||
| + | range from very small to very large. <math>10^{−6}, 10^{6}</math> are clearly preferable to 0.000001, 1000000 | ||
| + | respectively. The standard logarithmic units are Bel and dB (decibel). These are used to | ||
| + | represent unitless numbers like ratios of similar quantities. Weights or voltages can not | ||
| + | represented by Bel/dB; ratios of two weights or two voltages can be. Given a unitless number | ||
| + | <math>X</math>, its equivalents are | ||
| + | |||
| + | <math>X\equiv\log_{10} (X)\text{Bel}\equiv10\log_{10} (X) \text{dB} </math> | ||
| + | |||
| + | A few numbers worth remembering are | ||
| + | |||
| + | <math>10\equiv 10 \text{dB} </math> | ||
| + | |||
| + | <math>2\equiv 3\text{dB} </math> | ||
| + | |||
| + | <math>3\equiv 4.77\text{dB} </math> | ||
| + | |||
| + | To represent voltages (V) and powers (W) in the logarithmic scale, we need some | ||
| + | standardization of definitions. This standardization is provided by dBV for voltages and | ||
| + | dBW, dBm, dBμ for powers. | ||
| + | |||
| + | <math>X(\text{volts})=20\log_{10} \frac{X}{1\text{V}}\text{dBV}</math> | ||
| + | |||
| + | <math>X(\text{watts})\equiv 10\log_{10}\frac{X}{1\text{W}} \text{dBW}\equiv10\log_{10}\frac{X}{1\text{mW}}\text{dBm} \equiv 10\log_{10}\frac{X}{1\mu \text{W}}dB\mu</math> | ||
| + | |||
---- | ---- | ||
Revision as of 08:45, 23 August 2013
Contents
ECE 440 Lab 1
Experiment 1: Signals and Noise (1 week) (L1.pdf)
I. OBJECTIVES
Upon completion of this experiment, you should be able to:
1. Use the signal generators and filters in the lab to generate and filter noise and various types of periodic signals.
2. Characterize noise and periodic signals in the time and frequency domains by using the 54624A oscilloscope and the 4395A spectrum analyzer respectively.
3. Use the 8922A voltmeter to determine the RMS voltage (or equivalently, the power) of a signal.
II. INTRODUCTION
In this course, you will be studying communication systems and signals, and the effect of noise on these systems. You will frequently need to analyze signals (deterministic and random) in the time and frequency domains. This experiment introduces you to a number of instruments. These instruments include spectrum analyzers for frequency domain analysis, oscilloscopes for time domain analysis, and voltmeters, frequency counters., etc.
III. PRELAB
1. Define average power and root-mean-square value for deterministic signals.
2 State Parseval’s Theorem for periodic signals.
3. Define power, power spectral density, and autocorrelation for deterministic signals. Point out any relation between these. (Equations Only.)
4. Gaussian white noise, perfectly band-limited to 0-10MHz, is passed through a perfectly rectangular filter of bandwidth 18 kHz, gain 3 dB, and center frequency 455 kHz. If the RMS voltage of the input noise is 1 volt, what is the RMS voltage of the output noise?
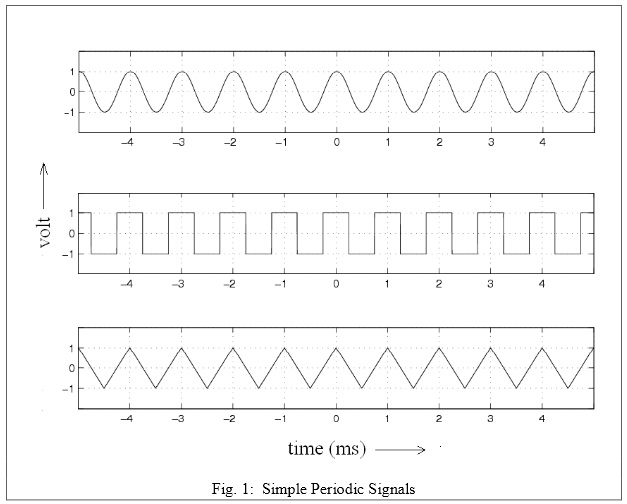
5. Consider the signals shown in Figure. 1. Each h as a period of 1ms.
5a. Determine the root mean square (RMS) value of each signal.
5b. Determine the RMS voltages associated with the first nine spectral components of the signal and complete the table provided. Show all calculations. You will need to provide t he answer in volts as well as dBV.
5c. Record results in Table 1. (Read the appendix for a review of dBV/dBm/dBW etc.)
Table 1
| Signal/RMS Voltage | Sine | Square | Triangular |
|---|---|---|---|
| RMS Voltage of DC Component | (V),(dBV) | (V),(dBV) | (V),(dBV) |
| RMS Voltage of 1kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) |
| RMS Voltage of 2kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) |
| RMS Voltage of 3kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) |
| RMS Voltage of 4kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) |
| RMS Voltage of 5kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) |
| RMS Voltage of 6kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) |
| RMS Voltage of 7kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) |
| RMS Voltage of 8kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) |
| Net RMS Voltage of spectral components up to 8kHz | (V),(dBV) | (V),(dBV) | (V),(dBV) |
| Total RMS Voltage | (V),(dBV) | (V),(dBV) | (V),(dBV) |
IV. EXPERIMENT
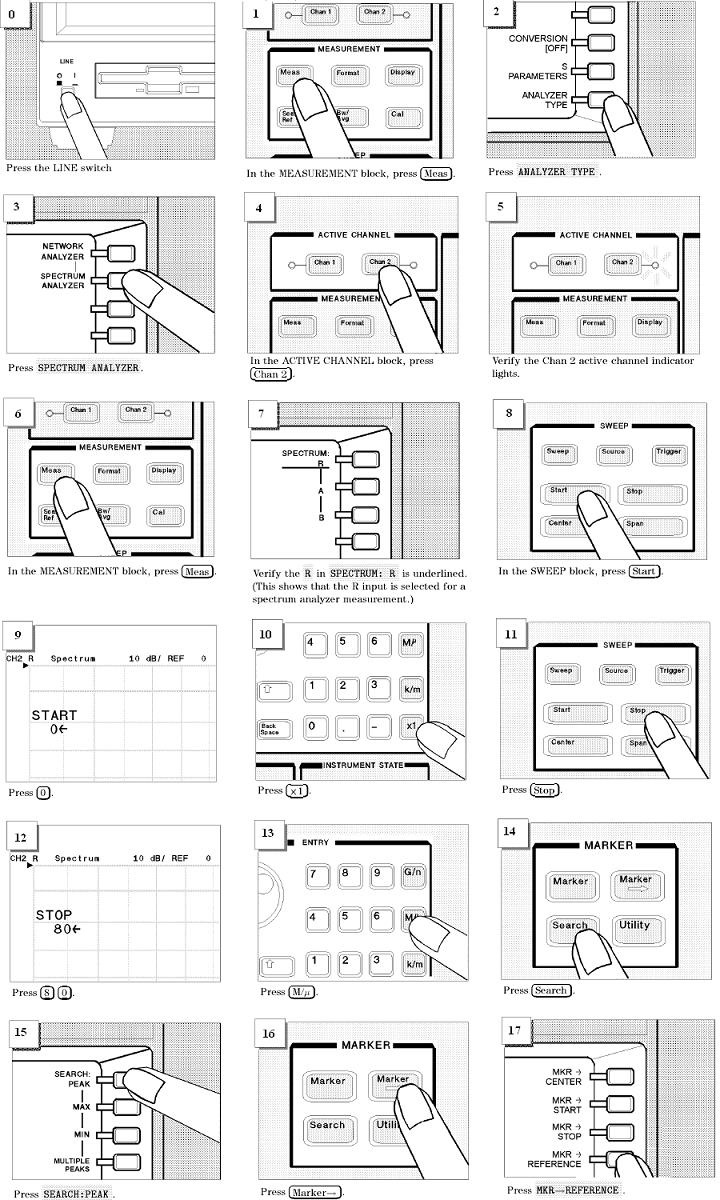
The goal of this experiment is to familiarize you to the Agilent 4395A SA, Fluke 8922A true RMS voltmeter, and the Agilent 54624A oscilloscope. An introduction to spectrum analyzers is in the Appendix. A ‘getting started’ guide to operating the 4395A is found in Figure 2.
1. Total Harmonic Distortion
Sinusoidal oscillators used in communication devices are not perfect. However, it is difficult to measure signal imperfections using an oscilloscope. For example, a 200 kHz sine wave oscillator will produce a dominant fundamental component at 200 kHz, small harmonics at integral multiples of 200 kHz, and, possibly, some small spurs at some other frequencies. These components can not be seen with an oscilloscope. A spectrum analyzer has extremely good dynamic range that allows us to measure these small components.
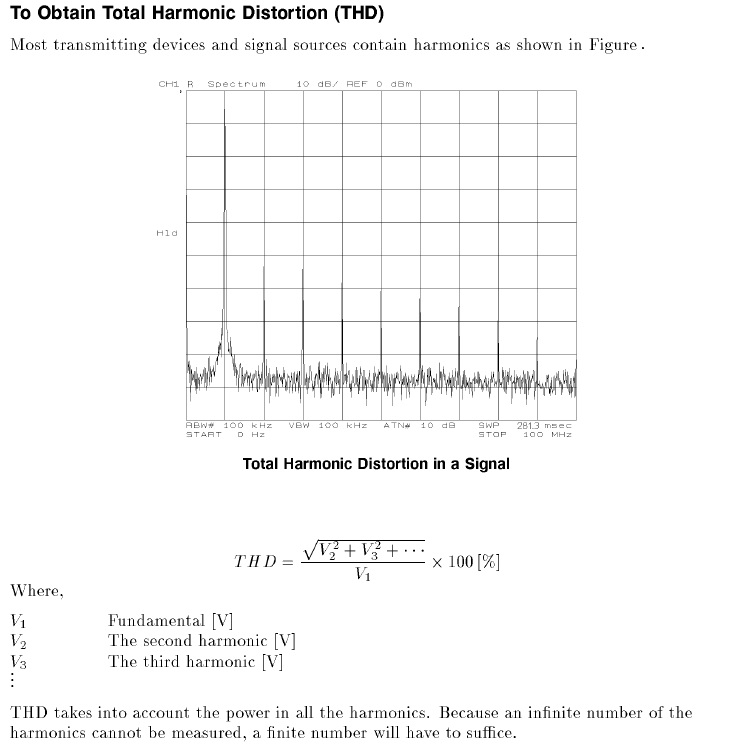
1 a. Use the spectrum analyzer to measure the total harmonic distortion (THD) of the HP200CD and HP3314A sinusoidal oscillators at 200 kHz (use 1Vp-p signals). The definition of THD is provided in Figure. 3.
NOTE: Before connecting any signal to the SA, observe it on the oscilloscope to ensure that the signal is as expected and has the correct amplitude.
NOTE: The spectrum analyzer cannot handle large input voltages.. - Always use a 40 dB attenuator between the signal and the SA input.
- The 40 dB attenuator is just a 4950Ω resistor. This resistor and the 50Ω input resistance of the SA form a 100:1 voltage divider at low frequencies.
- If at any point, the SA displays a ‘Caution: Overload on Input’ sign, disconnect the signal at the SA input and reduce all amplitudes.
2. Measuring the Spectra of Periodic Signals
2 a. Generate a triangular wave and a square wave of frequency 1 kHz and amplitude 1V; measure their spectra and compare to pre-lab results. Measure their RMS voltages using the 8922A and compare to theory. The 8922A is a ‘True RMS Voltmeter’. It is capable of providing readings in linear (V) and logarithmic (dBm) scales. (Set the Fluke meter to <AC> (no DC) mode to prevent DC offset errors.)
2 b. How would you obtain readings in dBV using the 8922A meter?
3. Measuring the Spectrum of Noise
3 a. Generate a 1V RMS noise signal with the 33220A and determine its power spectral density (PSD) in dBm/Hz as a function of frequency. Sketch it or obtain a print-out. ( Use the noise setting on your SA: <FORMAT>→<NOISE>. ) Do you understand this setting? If not, ask your TA.)
3 b. From the spectrum analyzer display, determine the approximate bandwidth of the noise generated by the 33220A. It should be approximately 9 MHz. Use the bandwidth and the PSD determined above to estimate the RMS voltage. Measure the RMS voltage with the Fluke 8922A (its BW is approximately 11 MHz). Compare.
3 c. Set the Krohn-Hite filter at your station to a Maximally Flat bandwidth of 1 MHz. The bandwidth and type (LPF or HPF) of filter can be set by knobs on the front. The filter response (RC vs. Maximally Flat) is determined by a switch on the back. Use the 1V RMS noise from the 33220A as input to this filter and estimate the PSD and RMS voltage of the output using the Spectrum Analyzer. Measure with 8922A. Repeat for a low-pass filter bandwidth of 2 MHz. Does doubling the bandwidth double the measured RMS voltage? (Careful) Discuss.
3 d. Do the measured RMS voltages agree with the PSD and bandwidth measurements?
3 e. Use the 1V RMS noise from the 33220A as input to the 455 kHz band-pass filter on your station and determine the PSD of the output noise process. Measure the RMS voltage of the output noise and compare to pre-lab results. For purposes of comparison, assume the 455 kHz BPF to be a brick-wall filter with a bandwidth of 18 kHz and a gain of 3 dB.
4. Measuring Signal-to-Noise ratios
A signal consisting of the sum of two sinusoids (at 100 kHz and 110 kHz) is corrupted with additive white Gaussian noise and is available on Jack B of the patch-panel on your station.
4 a. Use the 8922A and the spectrum analyzer to measure the signal-to-noise ratio.
Signal-to-Noise Ratio is the ratio of signal power to noise power.
$ \frac{S}{N}=\frac{\text{Signal Power}}{\text{Noise Power}}=\frac{(V_{rms},signal)^2}{(V_{rms},noise)^2} $
The signal power of the sum of two sinusoids, $ V_1(t) $ and $ V_2(t) $ is:
$ \text{Signal power} = V_{1,rms}^2+V_{2,rms}^2 $
4 b. Observe the effect of varying the VBW and RBW on the sinusoidal signals as well as the noise component. Record your observations in your lab report.
V. REPORT
Document all the readings you have obtained and any conclusions you draw in your report. Attach a copy of your lab record to the report. Answer any specific questions asked in the lab manual.
VI. APPENDIX
The logarithmic notation: Bels and decibels
The logarithmic notation provides an easy way to specify numbers and quantities that can range from very small to very large. $ 10^{−6}, 10^{6} $ are clearly preferable to 0.000001, 1000000 respectively. The standard logarithmic units are Bel and dB (decibel). These are used to represent unitless numbers like ratios of similar quantities. Weights or voltages can not represented by Bel/dB; ratios of two weights or two voltages can be. Given a unitless number $ X $, its equivalents are
$ X\equiv\log_{10} (X)\text{Bel}\equiv10\log_{10} (X) \text{dB} $
A few numbers worth remembering are
$ 10\equiv 10 \text{dB} $
$ 2\equiv 3\text{dB} $
$ 3\equiv 4.77\text{dB} $
To represent voltages (V) and powers (W) in the logarithmic scale, we need some standardization of definitions. This standardization is provided by dBV for voltages and dBW, dBm, dBμ for powers.
$ X(\text{volts})=20\log_{10} \frac{X}{1\text{V}}\text{dBV} $
$ X(\text{watts})\equiv 10\log_{10}\frac{X}{1\text{W}} \text{dBW}\equiv10\log_{10}\frac{X}{1\text{mW}}\text{dBm} \equiv 10\log_{10}\frac{X}{1\mu \text{W}}dB\mu $
Discussion/comments
- Put comment/question here
- answer here