| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Category:ECE440Fall2013Love]] | [[Category:ECE440Fall2013Love]] | ||
[[Category:ECE440]] | [[Category:ECE440]] | ||
| Line 130: | Line 98: | ||
<br> | <br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
--- | --- | ||
[[2013_Fall_ECE_440_Love|Back to Fall 2013 ECE 440]] | [[2013_Fall_ECE_440_Love|Back to Fall 2013 ECE 440]] | ||
Revision as of 07:51, 23 August 2013
Contents
ECE 440 Lab 1
Experiment 1: Signals and Noise (1 week) (L1.pdf)
I. OBJECTIVES
Upon completion of this experiment, you should be able to:
1. Use the signal generators and filters in the lab to generate and filter noise and various types of periodic signals.
2. Characterize noise and periodic signals in the time and frequency domains by using the 54624A oscilloscope and the 4395A spectrum analyzer respectively.
3. Use the 8922A voltmeter to determine the RMS voltage (or equivalently, the power) of a signal.
II. INTRODUCTION
In this course, you will be studying communication systems and signals, and the effect of noise on these systems. You will frequently need to analyze signals (deterministic and random) in the time and frequency domains. This experiment introduces you to a number of instruments. These instruments include spectrum analyzers for frequency domain analysis, oscilloscopes for time domain analysis, and voltmeters, frequency counters., etc.
III. PRELAB
1. Define average power and root-mean-square value for deterministic signals.
2 State Parseval’s Theorem for periodic signals.
3. Define power, power spectral density, and autocorrelation for deterministic signals. Point out any relation between these. (Equations Only.)
4. Gaussian white noise, perfectly band-limited to 0-10MHz, is passed through a perfectly rectangular filter of bandwidth 18 kHz, gain 3 dB, and center frequency 455 kHz. If the RMS voltage of the input noise is 1 volt, what is the RMS voltage of the output noise?
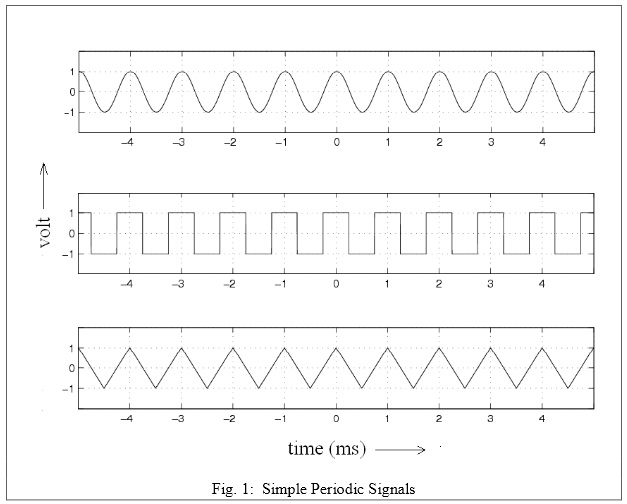
5. Consider the signals shown in Figure. 1. Each h as a period of 1ms.
5a. Determine the root mean square (RMS) value of each signal.
5b. Determine the RMS voltages associated with the first nine spectral components of the signal and complete the table provided. Show all calculations. You will need to provide t he answer in volts as well as dBV.
5c. Record results in Table 1. (Read the appendix for a review of dBV/dBm/dBW etc.)
| Signal/RMS Voltage | Sine | Square | Triangular | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMS Voltage of DC Component | (V),(dBV) | (V),(dBV) | (V),(dBV) | ||||||||||||||||||||||||||||||||||||
| RMS Voltage of 1kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) | RMS Voltage of 2kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) | RMS Voltage of 3kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) | RMS Voltage of 4kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) | RMS Voltage of 5kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) | RMS Voltage of 6kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) | RMS Voltage of 7kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) | RMS Voltage of 8kHz Component | (V),(dBV) | (V),(dBV) | (V),(dBV) | Net RMS Voltage of spectral components up to 8kHz | (V),(dBV) | (V),(dBV) | (V),(dBV) | Total RMS Voltage | (V),(dBV) | (V),(dBV) | (V),(dBV) |