Revision as of 06:50, 6 June 2013

1.1 Converting Integers to Binary

Introduction

Everyday we view numbers and use them for our work, studies or just for fun. The key factor is how we can understand these numbers and then use them. But how can we get a computer to recognize regular, everyday numbers such as 2013, 777 and 123? A basic computer cannot recognize these numbers in this form but we can change the form to a more logical, algorithmic form. This logical form which is known as binary has been made specifically for computers to be able to read and interpret numbers. This Slecture will describe how to convert normal everyday number format to binary.

Examples of binary and basic binary to integer translation

Binary uses only 2 numbers, 0 and 1. When dealing with logic situations and boolean algebra, 0 means 'false' and 1 means 'true'. A binary number can look like the following:

$ 001, 1011, 10101010101, \text{ etc.} $

Also, there is no limit to how big these binary numbers can be.

Before we can begin converting, we have to figure out how binary works. Lets analyze what each 0 and 1 represents in a few strings of binary.

$ 11111 = 1*2^4+1*2^3+1*2^2+1*2^1+1*2^0 = 16+8+4+2+1 = 31 $

As shown above, each integer (each 1 in this case) represents a product (you mean power? )of 2. Starting from the right to the left, the exponent of 2 increments from 0 to the length of the binary term minus 1.

Lastly its important to notice that if a product of 2 is represented with a 0, you multiply that product of 2 with 0 or simply ignore it in your adding process. With this knowledge, we can begin converting binary to regular numbers.

Example: Convert 1011 to a number.

Solution: $ 1\times 2^3+0\times 2^2+1\times 2^1+1 \times 2^0 = 8+0+2+1 = 11 $

Recognizing different bases of numbers and binary

Numbers that we use everyday, like 7 and 9 are base 10, which means the ones, tenths, hundredths, etc can go from 0 to 9.

Example of counting up a base 3 number: 0, 1, 2, 10, 11, 12, 10, 20, 21, 22, 100, 101,.....

Noticed how the tenths digit stopped at the twenties? This is because it is base 3, in which the tenths can only go from 0 to 2. If we continue this counting process, we will reach 1000 much more quickly than a base 10 number.

The largest base of numbers is base 16 which is from 0-F, meaning 0-9, A, B, C, D, E, F.

It is important to note that base 16 numbers will be used extensively for microprocessors and other types of computer design.

Base 10 to base 16 conversion example

These conversions may seem tricky but there is a solid method to performing these conversions.

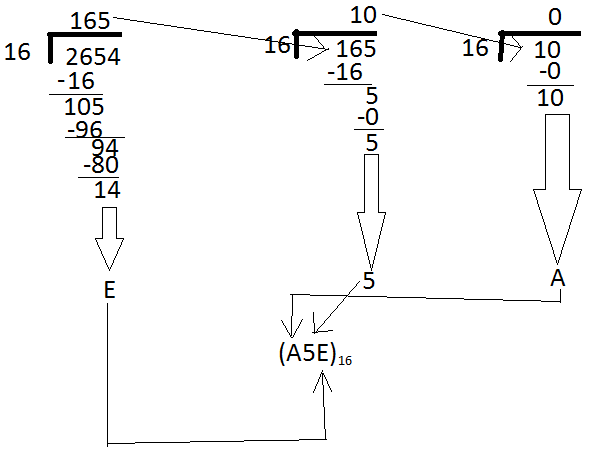
Example: Convert (2654)₁₀ to base 16

      Notice how the remainders are the base 16 numbers we are looking for and that the quotients get passed down to another set of dividers and continues until the last quotient is 0.

Back to table of content for "The Brown-Meyer Lectures on Digital Systems Design"