| Line 13: | Line 13: | ||
---- | ---- | ||
---- | ---- | ||
| − | == | + | ==Introduction== |
| − | + | I was taking ECE 302, a course on probability, random variables, and random processes, when all of a sudden I got overwhelmed with all of these different statistical numbers describing relations of datasets or random variables. So, I decided to crack down on some research and bring the important ideas all in one spot so that future students (or anyone for that matter) can quickly understand the differences between these functions. Feel free to comment and ask questions | |
| − | + | ==Definitions== | |
| − | + | '''Variation:''' This is used to analyze the factors that affect the spread of the data being observed. [3] | |
| − | + | '''Standard Deviation:''' This is a measure of how spread out a set of numeric values is about its mean. [3] | |
| + | '''Covariance:''' This is a measure of two random variable’s association with each other.[3] | ||
| − | Correlation is | + | '''Correlation:''' This is the degree to which two random variables vary with each other.[3] |
| + | |||
| + | '''Autocovariance:''' This is the measure of two data points of a random variable’s association with each other | ||
| + | |||
| + | '''Autocorrelation:''' This is the degree to which two data points of a random variable vary with each other | ||
| + | |||
| + | ==Mathematical Definitions== | ||
| + | |||
| + | '''Variation:''' | ||
| + | |||
| + | <math> | ||
| + | Var(X) = E[(X-\mu)(X-\mu)] = E[(X-\mu)^{2}] | ||
| + | </math> | ||
| + | |||
| + | Looking ahead, the variance of X, Var(X), is can also be described as the covariance of X with X, Cov(X,X). If you go to the covariance definition and use the variable X instead of Y, you will obtain the definition of variance. Another popular way of defining variance is | ||
| + | |||
| + | <math> | ||
| + | Var(X) = E[X^{2}] - (E[X])^{2} | ||
| + | </math> | ||
| + | |||
| + | This is derived by manipulating the definition above using the rules | ||
| + | of expected value. | ||
| + | |||
| + | '''Standard Deviation:''' | ||
| + | |||
| + | <math> | ||
| + | \sigma = \sqrt{E[(X-\mu)^{2}]} = \sqrt{Var(X)} | ||
| + | </math> | ||
| + | |||
| + | The standard deviation is simply the square root of the variance. | ||
| + | |||
| + | '''Covariance:''' | ||
| + | |||
| + | <math> | ||
| + | \sigma(X,Y) = E[(X-\mu_{x})(Y-\mu_{y})] | ||
| + | </math> | ||
| + | |||
| + | Remember that the covariance is a relation of two random variables, X and Y. As it was mentioned previously, if you find the covariance of X and X, you will simply obtain the variance of X | ||
| + | |||
| + | '''Correlation:''' | ||
| + | |||
| + | <math> | ||
| + | \rho_{X,Y} = \frac{cov(X,Y)}{\sigma_{X}\sigma_{Y}} = \frac{E[(X-\mu_{X})(Y-\mu_{Y})]}{\sigma_{X}\sigma_{Y}} | ||
| + | </math> | ||
| + | |||
| + | This puts the covariance on terms that is more understandable and quickly comparable. An example of this will be shown more clearly in the walkthrough. | ||
| + | |||
| + | '''Autocovariance:''' | ||
| + | |||
| + | <math> | ||
| + | \sigma_{X_{1}X_{2}}(n1,n2) = E[(X_{1}-\mu_{n1})(X_{2}-\mu_{n2})] | ||
| + | </math> | ||
| + | |||
| + | The autocovariance is just like the formula for covariance but instead of finding the relation of two random variables, you are finding the relation of two data points from one random variable. | ||
| + | |||
| + | '''Autocorrelation:''' | ||
| + | |||
| + | <math> | ||
| + | \rho_{X_{1},X_{2}} = \frac{cov(X_{1},X_{2})}{\sigma_{X_{1}}\sigma_{X_{2}}} = \frac{E[(X_{1}-\mu_{X_{1}})(X_{2}-\mu_{X_{2}})]}{\sigma_{X_{1}}\sigma_{X_{2}}} | ||
| + | </math> | ||
| + | |||
| + | This is like the correlation formula except it also finds the relation of two data points from one random variable instead of finding the relation of two random variables. | ||
| + | |||
| + | ==Walkthrough== | ||
| + | |||
| + | To start off, I will walk through the calculations of variation and standard deviation on a sample data set: | ||
| − | |||
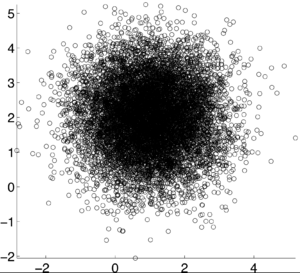
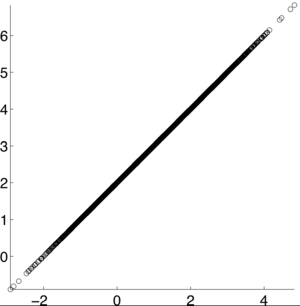
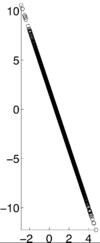
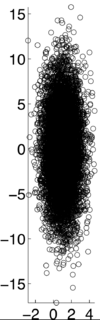
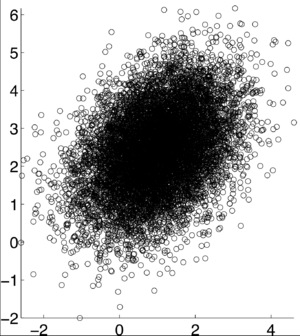
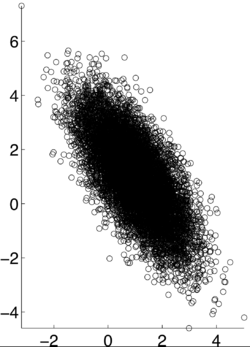
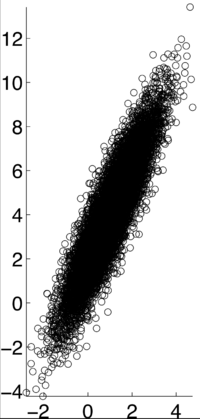
If X and Y are independent of each other, that means they are uncorrelated with each other, or cov(X,Y) = 0. However, if X and Y are uncorrelated, that does not mean they are independent of each other. 1, -1, and 0 are the three extreme points <math>p\rho X,Y)</math> can represent. 1 represents that X and Y are linearly dependent of each other. In other words, Y-E[Y] is a positive multiple of X-E[X]. -1 represents that X and Y are inversely dependent of each other. In other words, Y-E[Y] is a negative multiple of X-E[X]. [1] | If X and Y are independent of each other, that means they are uncorrelated with each other, or cov(X,Y) = 0. However, if X and Y are uncorrelated, that does not mean they are independent of each other. 1, -1, and 0 are the three extreme points <math>p\rho X,Y)</math> can represent. 1 represents that X and Y are linearly dependent of each other. In other words, Y-E[Y] is a positive multiple of X-E[X]. -1 represents that X and Y are inversely dependent of each other. In other words, Y-E[Y] is a negative multiple of X-E[X]. [1] | ||
| Line 53: | Line 118: | ||
<math>\rho (X,Y) = .9</math> [1] | <math>\rho (X,Y) = .9</math> [1] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
---- | ---- | ||
| Line 66: | Line 124: | ||
[2]: Ilya Pollak. Random Signals. 2004. Retrieved from https://engineering.purdue.edu/~ipollak/ee438/FALL04/notes/Section2.1.pdf | [2]: Ilya Pollak. Random Signals. 2004. Retrieved from https://engineering.purdue.edu/~ipollak/ee438/FALL04/notes/Section2.1.pdf | ||
| + | |||
| + | [3]: Dictionary.com Retrieved from https://www.dictionary.com | ||
[[2013_Spring_ECE_302_Boutin|Back to ECE302 Spring 2013, Prof. Boutin]] | [[2013_Spring_ECE_302_Boutin|Back to ECE302 Spring 2013, Prof. Boutin]] | ||
Revision as of 04:10, 5 May 2013
Correlation vs Covariance
Student project for ECE302
by Blue
Contents
Introduction
I was taking ECE 302, a course on probability, random variables, and random processes, when all of a sudden I got overwhelmed with all of these different statistical numbers describing relations of datasets or random variables. So, I decided to crack down on some research and bring the important ideas all in one spot so that future students (or anyone for that matter) can quickly understand the differences between these functions. Feel free to comment and ask questions
Definitions
Variation: This is used to analyze the factors that affect the spread of the data being observed. [3]
Standard Deviation: This is a measure of how spread out a set of numeric values is about its mean. [3]
Covariance: This is a measure of two random variable’s association with each other.[3]
Correlation: This is the degree to which two random variables vary with each other.[3]
Autocovariance: This is the measure of two data points of a random variable’s association with each other
Autocorrelation: This is the degree to which two data points of a random variable vary with each other
Mathematical Definitions
Variation:
$ Var(X) = E[(X-\mu)(X-\mu)] = E[(X-\mu)^{2}] $
Looking ahead, the variance of X, Var(X), is can also be described as the covariance of X with X, Cov(X,X). If you go to the covariance definition and use the variable X instead of Y, you will obtain the definition of variance. Another popular way of defining variance is
$ Var(X) = E[X^{2}] - (E[X])^{2} $
This is derived by manipulating the definition above using the rules of expected value.
Standard Deviation:
$ \sigma = \sqrt{E[(X-\mu)^{2}]} = \sqrt{Var(X)} $
The standard deviation is simply the square root of the variance.
Covariance:
$ \sigma(X,Y) = E[(X-\mu_{x})(Y-\mu_{y})] $
Remember that the covariance is a relation of two random variables, X and Y. As it was mentioned previously, if you find the covariance of X and X, you will simply obtain the variance of X
Correlation:
$ \rho_{X,Y} = \frac{cov(X,Y)}{\sigma_{X}\sigma_{Y}} = \frac{E[(X-\mu_{X})(Y-\mu_{Y})]}{\sigma_{X}\sigma_{Y}} $
This puts the covariance on terms that is more understandable and quickly comparable. An example of this will be shown more clearly in the walkthrough.
Autocovariance:
$ \sigma_{X_{1}X_{2}}(n1,n2) = E[(X_{1}-\mu_{n1})(X_{2}-\mu_{n2})] $
The autocovariance is just like the formula for covariance but instead of finding the relation of two random variables, you are finding the relation of two data points from one random variable.
Autocorrelation:
$ \rho_{X_{1},X_{2}} = \frac{cov(X_{1},X_{2})}{\sigma_{X_{1}}\sigma_{X_{2}}} = \frac{E[(X_{1}-\mu_{X_{1}})(X_{2}-\mu_{X_{2}})]}{\sigma_{X_{1}}\sigma_{X_{2}}} $
This is like the correlation formula except it also finds the relation of two data points from one random variable instead of finding the relation of two random variables.
Walkthrough
To start off, I will walk through the calculations of variation and standard deviation on a sample data set:
If X and Y are independent of each other, that means they are uncorrelated with each other, or cov(X,Y) = 0. However, if X and Y are uncorrelated, that does not mean they are independent of each other. 1, -1, and 0 are the three extreme points $ p\rho X,Y) $ can represent. 1 represents that X and Y are linearly dependent of each other. In other words, Y-E[Y] is a positive multiple of X-E[X]. -1 represents that X and Y are inversely dependent of each other. In other words, Y-E[Y] is a negative multiple of X-E[X]. [1]
Examples
References
[1]: Ilya Pollak. General Random Variables. 2012. Retrieved from https://engineering.purdue.edu/~ipollak/ece302/SPRING12/notes/19_GeneralRVs-4_Multiple_RVs.pdf
[2]: Ilya Pollak. Random Signals. 2004. Retrieved from https://engineering.purdue.edu/~ipollak/ee438/FALL04/notes/Section2.1.pdf
[3]: Dictionary.com Retrieved from https://www.dictionary.com