| Line 3: | Line 3: | ||
[[Category:Impulse Response]] | [[Category:Impulse Response]] | ||
| + | <center><font size= 4> | ||
| + | '''TITLE''' | ||
| + | </font size> | ||
| + | |||
| + | Student project for [[ECE301]] | ||
| + | </center> | ||
| + | ---- | ||
| + | ---- | ||
Impulse Response: mathematically the impulse response can be modeled as a dirac delta function. The dirac delta represents an infinitely short pulse that has an infinitely high peak. The function itself exists as a mathematical object only when present in an integral. It is a measure that approximates the 0 value of the function that it multiplies with in the integral. The dirac delta function can be used to solve differential equations, because the convolution of a function with the delta function is itself. | Impulse Response: mathematically the impulse response can be modeled as a dirac delta function. The dirac delta represents an infinitely short pulse that has an infinitely high peak. The function itself exists as a mathematical object only when present in an integral. It is a measure that approximates the 0 value of the function that it multiplies with in the integral. The dirac delta function can be used to solve differential equations, because the convolution of a function with the delta function is itself. | ||
Latest revision as of 16:45, 21 April 2013
TITLE
Student project for ECE301
Impulse Response: mathematically the impulse response can be modeled as a dirac delta function. The dirac delta represents an infinitely short pulse that has an infinitely high peak. The function itself exists as a mathematical object only when present in an integral. It is a measure that approximates the 0 value of the function that it multiplies with in the integral. The dirac delta function can be used to solve differential equations, because the convolution of a function with the delta function is itself.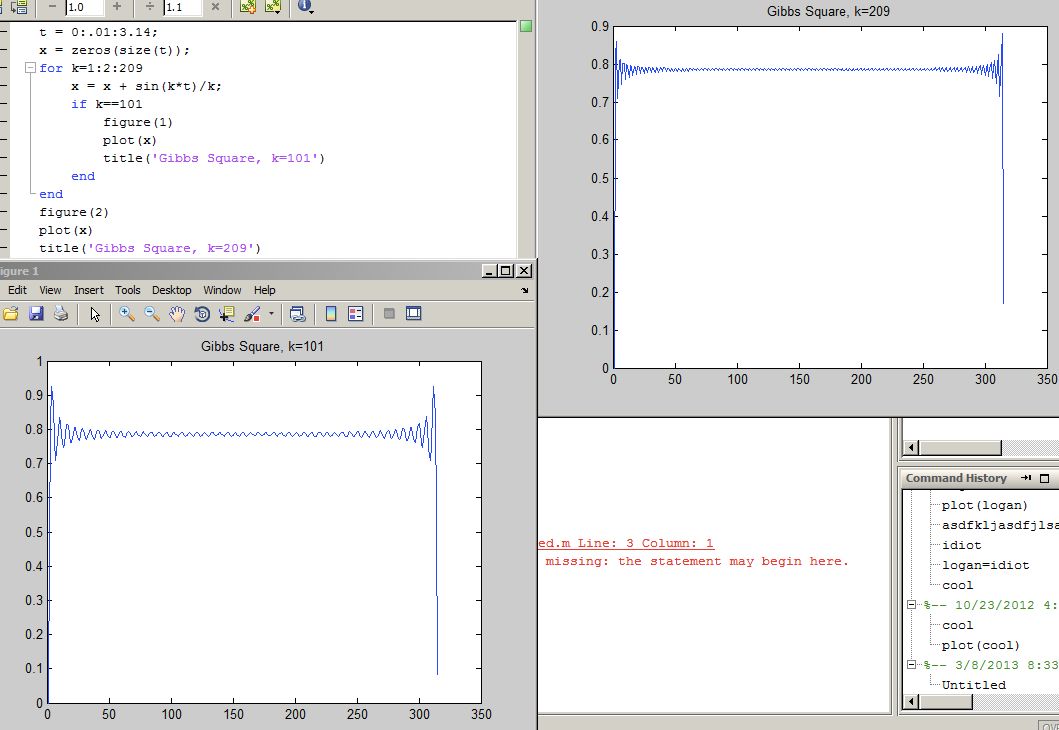
The overshoot increases as the number of coefficients summed increases.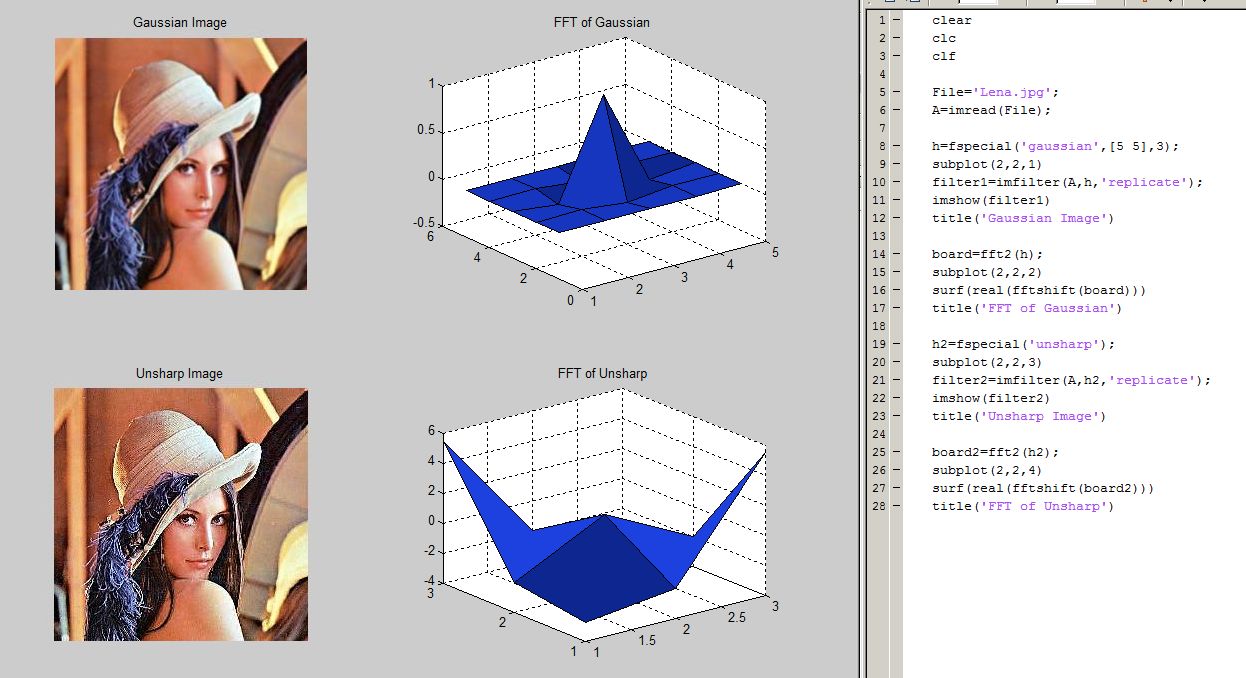
The gaussian filter blurs the image. The high frequency filtering removes noise, but also blurs images as a result. The unsharp filter accentuates the edges of images, in an emboss like feature. The parts of the image are most apparent in the hat and the blue curls stemming from it.

