| Line 62: | Line 62: | ||
e) We are likely to see quantization artifact in dark region. | e) We are likely to see quantization artifact in dark region. | ||
| + | |||
| + | == Solution From Another Student: == | ||
| + | |||
| + | a) The gamma is 1 | ||
| + | |||
| + | b) | ||
| + | |||
| + | <math> | ||
| + | (x_r,y_r)=(\frac{a}{a+d+g},\frac{d}{a+d+g}) | ||
| + | </math> <br \> | ||
| + | <math> | ||
| + | (x_g,y_g)=(\frac{b}{b+e+h},\frac{e}{b+e+h}) | ||
| + | </math><br \> | ||
| + | <math> | ||
| + | (x_b,y_b)=(\frac{c}{c+f+i},\frac{f}{c+f+i}) | ||
| + | </math> | ||
| + | |||
| + | c) | ||
| + | |||
| + | <math> | ||
| + | (x_w,y_w)=(\frac{a+b+c}{a+b+c+d+e+f+g+h+i},\frac{d+e+f}{a+b+c+d+e+f+g+h+i}) | ||
| + | </math> | ||
| + | |||
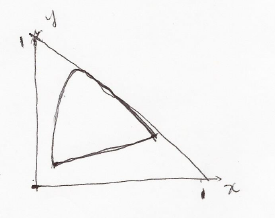
| + | d) This color is imaginary. At least one of R,G,B values must be negative. Cannot be produced by this device. [[ Image:Pro1_d2.PNG ]]<br /> | ||
| + | |||
| + | e) Quantization artifacts in the dark area. | ||
| + | |||
---- | ---- | ||
[[ECE_PhD_Qualifying_Exams|Back to ECE QE page]]: | [[ECE_PhD_Qualifying_Exams|Back to ECE QE page]]: | ||
Revision as of 16:50, 18 March 2013
Contents
ECE Ph.D. Qualifying Exam: CS-5 (637)
- Problem 1 , 2
Problem 1
Consider the emissive display device which is accurately modeled by the equation
$ \left[ {\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} a&b&c\\ d&e&f\\ g&h&i \end{array}} \right]\left[ {\begin{array}{*{20}{c}} R\\ G\\ B \end{array}} \right] $
where R, G and B are the red, green, and blue inputs in the range 0 to 255 that are used to modulate physically realizable color primaries.
a) What is the gamma of the device?
b) What are the chromaticity components $ (x_r,y_r), (x_g,y_g) $ and $ (x_b,y_b) $ of the device's three primaries.
c) What are the chromaticity components $ (x_w,y_w) $ of the device's white point.
d) If $ (X,Y,Z)=(0,1/2,1/2) $, then what can you say about the values of $ (R,G,B) $? (Hint: Draw a chromaticity diagram to find the answer.)
e) Imagine that the values of $ (R,G,B) $ are quantized to 8 bits, and that you view a smooth gradient from black to white on this device. What artifact are you likely to see, and where in the gradient will you see it?
Solution:
a) $ \gamma=1 $
b)
$ (x_r,y_r)=(\frac{a}{a+d+g},\frac{d}{a+d+g}) $
$ (x_g,y_g)=(\frac{b}{b+e+h},\frac{e}{b+e+h}) $
$ (x_b,y_b)=(\frac{c}{c+f+i},\frac{f}{c+f+i}) $
c)
$ (x_w,y_w)=(\frac{a+b+c}{a+b+c+d+e+f+g+h+i},\frac{d+e+f}{a+b+c+d+e+f+g+h+i}) $
d)
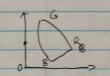
If $ (X,Y,Z)=(0,1/2,1/2) $, then $ (x,y)=(0,1/2) $.
In the chromaticity diagram, this point is outside the horse shoe shape, wo its RGB values are not all larger than 0 ($ R<0,G>0,B>0 $).
e) We are likely to see quantization artifact in dark region.
Solution From Another Student:
a) The gamma is 1
b)
$ (x_r,y_r)=(\frac{a}{a+d+g},\frac{d}{a+d+g}) $
$ (x_g,y_g)=(\frac{b}{b+e+h},\frac{e}{b+e+h}) $
$ (x_b,y_b)=(\frac{c}{c+f+i},\frac{f}{c+f+i}) $
c)
$ (x_w,y_w)=(\frac{a+b+c}{a+b+c+d+e+f+g+h+i},\frac{d+e+f}{a+b+c+d+e+f+g+h+i}) $
d) This color is imaginary. At least one of R,G,B values must be negative. Cannot be produced by this device.
e) Quantization artifacts in the dark area.