(New page: Image:Curve example.png Image:Curve example with x.png Image:Curve example with x and arrow.png Image:Curve example with y and arrow.png) |
|||
| Line 1: | Line 1: | ||
| + | |||
| + | [[Category:math]] | ||
| + | [[Category:tutorial]] | ||
| + | |||
| + | == The County Problem - A Topological Argument == | ||
| + | <pre> keyword: tutorial, inside county, closed curve, curve </pre> | ||
| + | |||
| + | '''INTRODUCTION''' In this tutorial / exploration, I'll talk a little about topology, and a little about programming, with the goal of showing you that thinking mathematically can really get you out of a pickle sometimes. | ||
| + | |||
| + | <pre> Contents | ||
| + | - The Problem | ||
| + | - The Solution | ||
| + | - Why it works | ||
| + | - References | ||
| + | </pre> | ||
| + | ---- | ||
| + | ==The problem== | ||
| + | |||
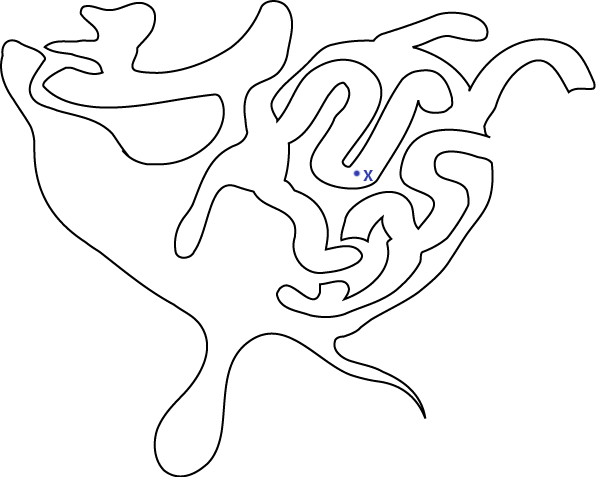
| + | The problem we want to solve here is as follows: we want to create a computer function which takes an Indiana longitude and latitude value as input, and returns the county in which this point lies. At first this seems like a rather simple problem, for when one looks at a county and some point inside the county, they can immediately see whether the point is inside the county. For example: | ||
| + | |||
| + | |||
| + | |||
| + | The problem I will tackle here is very specific, and applicable to many areas of computer programming. I stumbled upon it when I was working on storing map data in a database. The problem was I had a database of address information which was stored as just a text entry. In other words, the data for a given address was just a string, such as "EXAMPLE ADDRESS". We wanted to add and we needed to get from this information | ||
| + | |||
| + | Lorem Ipsum [1] is simply dummy text of the printing and typesetting industry. Lorem Ipsum has been the industry's standard dummy text ever since the 1500s, when an unknown printer took a galley of type and scrambled it to make a type specimen book. It has survived not only five centuries, but also the leap into electronic typesetting, remaining essentially unchanged. It was popularised in the 1960s with the release of Letraset sheets containing Lorem Ipsum passages, and more recently with desktop publishing software like Aldus PageMaker including versions of Lorem Ipsum. | ||
| + | ---- | ||
| + | ==The solution== | ||
| + | |||
| + | Lorem Ipsum [1] is simply dummy text of the printing and typesetting industry. Lorem Ipsum has been the industry's standard dummy text ever since the 1500s, when an unknown printer took a galley of type and scrambled it to make a type specimen book. It has survived not only five centuries, but also the leap into electronic typesetting, remaining essentially unchanged. It was popularised in the 1960s with the release of Letraset sheets containing Lorem Ipsum passages, and more recently with desktop publishing software like Aldus PageMaker including versions of Lorem Ipsum. | ||
| + | ---- | ||
| + | ==Why it works== | ||
| + | |||
| + | Now why does this work? It seems like a magical fact which I just pulled out of my pocket. But the great thing about this particular mathematical fact is that it's something which we can easily argue. So here I'll present the outline of a proof. The idea is that if we were to take a large circle, we can bend continuously, and with rather strict rules, into an arbitrary simple, closed curve (a curve which is simple and curved is commonly called a [[http://mathworld.wolfram.com/JordanCurve.html|Jordan Curve]]). These strict rules preserve a specific property of the curve which corresponds to the insideness of the chosen point. | ||
| + | |||
| + | Imagine you start with some arbitrary curve in the plane, and you're interested in whether a point is inside or outside the curve: | ||
| + | |||
| + | [[Image:Curve example with x.png]] | ||
| + | |||
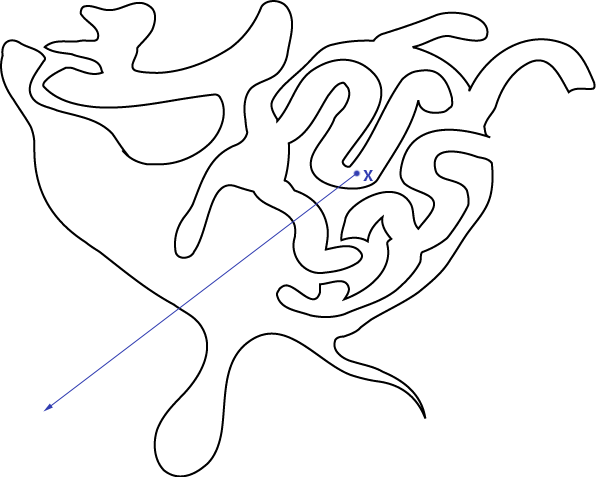
| + | Now imagine you draw a ray from that point in an arbitrary direction in the plane, and that we focus on the number of intersections that line makes with the sides or the curve: | ||
| + | |||
| + | [[Image:Curve example with x and arrow.png]] | ||
| + | |||
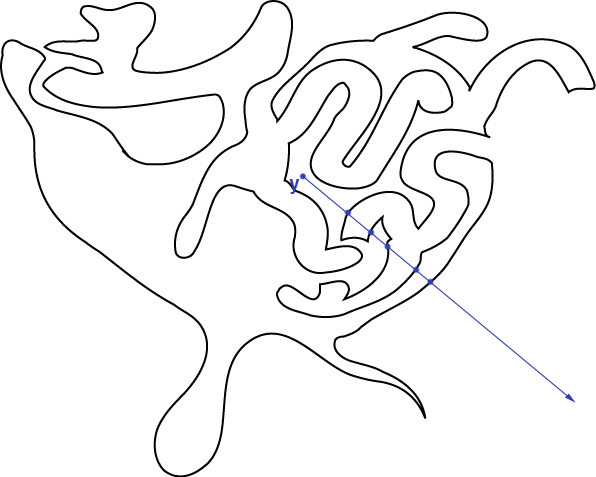
| + | It is not yet clear what the relationship is between the number of intersections and the insideness of the point, but we can try to reduce the situation to a simpler situation. Imagine the various deformations of the curve which preserve insideness and the effect these has on the number of intersections: | ||
| + | |||
| + | '' | ||
| + | |||
| + | |||
| + | ---- | ||
| + | ==REFERENCES== | ||
| + | [1] "Loream Ipsum" <http://www.lipsum.com/>. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | [[Math_squad|Back to Math Squad page]] | ||
| + | |||
| + | |||
| + | |||
[[Image:Curve example.png]] | [[Image:Curve example.png]] | ||
Revision as of 11:43, 11 March 2013
Contents
The County Problem - A Topological Argument
keyword: tutorial, inside county, closed curve, curve
INTRODUCTION In this tutorial / exploration, I'll talk a little about topology, and a little about programming, with the goal of showing you that thinking mathematically can really get you out of a pickle sometimes.
Contents - The Problem - The Solution - Why it works - References
The problem
The problem we want to solve here is as follows: we want to create a computer function which takes an Indiana longitude and latitude value as input, and returns the county in which this point lies. At first this seems like a rather simple problem, for when one looks at a county and some point inside the county, they can immediately see whether the point is inside the county. For example:
The problem I will tackle here is very specific, and applicable to many areas of computer programming. I stumbled upon it when I was working on storing map data in a database. The problem was I had a database of address information which was stored as just a text entry. In other words, the data for a given address was just a string, such as "EXAMPLE ADDRESS". We wanted to add and we needed to get from this information
Lorem Ipsum [1] is simply dummy text of the printing and typesetting industry. Lorem Ipsum has been the industry's standard dummy text ever since the 1500s, when an unknown printer took a galley of type and scrambled it to make a type specimen book. It has survived not only five centuries, but also the leap into electronic typesetting, remaining essentially unchanged. It was popularised in the 1960s with the release of Letraset sheets containing Lorem Ipsum passages, and more recently with desktop publishing software like Aldus PageMaker including versions of Lorem Ipsum.
The solution
Lorem Ipsum [1] is simply dummy text of the printing and typesetting industry. Lorem Ipsum has been the industry's standard dummy text ever since the 1500s, when an unknown printer took a galley of type and scrambled it to make a type specimen book. It has survived not only five centuries, but also the leap into electronic typesetting, remaining essentially unchanged. It was popularised in the 1960s with the release of Letraset sheets containing Lorem Ipsum passages, and more recently with desktop publishing software like Aldus PageMaker including versions of Lorem Ipsum.
Why it works
Now why does this work? It seems like a magical fact which I just pulled out of my pocket. But the great thing about this particular mathematical fact is that it's something which we can easily argue. So here I'll present the outline of a proof. The idea is that if we were to take a large circle, we can bend continuously, and with rather strict rules, into an arbitrary simple, closed curve (a curve which is simple and curved is commonly called a [Curve]). These strict rules preserve a specific property of the curve which corresponds to the insideness of the chosen point.
Imagine you start with some arbitrary curve in the plane, and you're interested in whether a point is inside or outside the curve:
Now imagine you draw a ray from that point in an arbitrary direction in the plane, and that we focus on the number of intersections that line makes with the sides or the curve:
It is not yet clear what the relationship is between the number of intersections and the insideness of the point, but we can try to reduce the situation to a simpler situation. Imagine the various deformations of the curve which preserve insideness and the effect these has on the number of intersections:
REFERENCES
[1] "Loream Ipsum" <http://www.lipsum.com/>.