Line 42: Line 42:
 
</math>
 
</math>
  
 +
 +
<math>
 +
= z \text{ when } \left\{\begin{matrix}
 +
r cos \theta - z sin \theta = 0
 +
\\
 +
r sin \theta + z cos \theta = 0
 +
\end{matrix}\right.
 +
</math>
 +
 +
 +
<math>
 +
= \frac{r cos\theta}{sin \theta}, \theta > 0
 +
</math>
 +
 +
<math>{\color{red}
 +
\text{This answer is incorrect. The correct answer is as following:}}
 +
</math>
  
 
<math>{\color{green}
 
<math>{\color{green}
Line 63: Line 80:
  
  
−
<font face="serif"><span style="font-size: 19px;"><math>
+
<font face="serif"><span style="font-size: 19px;"><math>\color{green}
 
\text{ Define } u = r cos\theta - z sin\theta
 
\text{ Define } u = r cos\theta - z sin\theta
 
</math></span></font>
 
</math></span></font>
  
  
−
<math>
+
<math>\color{green}
 
\Rightarrow dz = \frac{du}{|sin\theta|}
 
\Rightarrow dz = \frac{du}{|sin\theta|}
 
</math>
 
</math>
  
  
−
<font face="serif"><span style="font-size: 19px;"><math>
+
<font face="serif"><span style="font-size: 19px;"><math>\color{green}
 
\text{ Now }
 
\text{ Now }
 
</math></span></font>
 
</math></span></font>
  
  
−
<math>
+
<math>\color{green}
 
p_{\theta}(r)  = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz}
 
p_{\theta}(r)  = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz}
 
</math>
 
</math>
  
  
−
<math>
+
<math>\color{green}
 
p_{\theta}(r)  = \int_{-\infty}^{+\infty}{\delta(g(u)) \delta(u) \frac{du}{|sin\theta|}} = \frac{\delta(u=0)}{|sin\theta|}
 
p_{\theta}(r)  = \int_{-\infty}^{+\infty}{\delta(g(u)) \delta(u) \frac{du}{|sin\theta|}} = \frac{\delta(u=0)}{|sin\theta|}
 
</math>
 
</math>
  
  
−
<math>
+
<math>\color{green}
 
= \frac{\delta(\frac{r}{sin\theta})}{|sin\theta|} = \frac{|sin\theta|}{|sin\theta|} \delta(r) = \delta(r)
 
= \frac{\delta(\frac{r}{sin\theta})}{|sin\theta|} = \frac{|sin\theta|}{|sin\theta|} \delta(r) = \delta(r)
 
</math>
 
</math>
Line 123: Line 140:
 
</math>
 
</math>
  
 +
<math>
 +
= z \text{ when } \left\{\begin{matrix}
 +
r cos \theta - z sin \theta = 1
 +
\\
 +
r sin \theta + z cos \theta = 1
 +
\end{matrix}\right.
 +
</math>
  
−
<font face="serif"><span style="font-size: 19px;"><math>
+
 
 +
<math>
 +
= \frac{r cos\theta - 1}{sin \theta}, \theta > 0
 +
</math>
 +
 
 +
<math>{\color{red}
 +
\text{This answer is incorrect. The correct answer is as following:}}
 +
</math>
 +
 
 +
<font face="serif"><span style="font-size: 19px;"><math>\color{green}
 
\text{ Similar to the solution 1 to part a) we define u: } u = r cos\theta - z sin\theta - 1  
 
\text{ Similar to the solution 1 to part a) we define u: } u = r cos\theta - z sin\theta - 1  
 
</math></span></font>
 
</math></span></font>
  
  
−
<font face="serif"><span style="font-size: 19px;"><math>
+
<font face="serif"><span style="font-size: 19px;"><math>\color{green}
 
\text{ Following the same logic as in part a) we obtain the final answer:}
 
\text{ Following the same logic as in part a) we obtain the final answer:}
 
</math></span></font>
 
</math></span></font>
  
  
−
<math>
+
<math>\color{green}
 
p_{\theta}(r)  = \delta(r - (cos\theta + sin \theta)) = \delta(r - \sqrt{2} cos (\theta - \frac{\pi}{4}))
 
p_{\theta}(r)  = \delta(r - (cos\theta + sin \theta)) = \delta(r - \sqrt{2} cos (\theta - \frac{\pi}{4}))
 
</math>
 
</math>
Line 179: Line 212:
  
 
<math>\color{green}
 
<math>\color{green}
−
\text{Recall:}
+
\text{Recall should be added:}
 
</math>
 
</math>
  

Revision as of 19:58, 2 August 2012

ECE Ph.D. Qualifying Exam in "Communication, Networks, Signal, and Image Processing" (CS)

Question 1, August 2011, Part 1

Part 1,2]

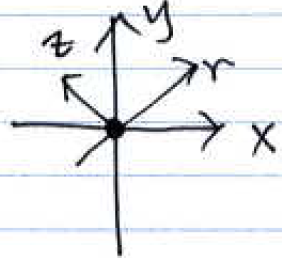
 $ \color{blue}\text{Consider an image } f(x,y) \text{ with a forward projection} $

                $ \color{blue} p_{\theta}(r) = \mathcal{FP}\left \{ f(x,y) \right \} $

                             $ \color{blue} = \int_{-\infty}^{\infty}{f \left ( r cos(\theta) - z sin(\theta),r sin(\theta) + z cos(\theta) \right )dz}. $

$ \color{blue} \text{Let } F(\mu,\nu) \text{ be the continuous-time Fourier transform of } f(x,y) \text{ given by} $
              $ \color{blue} F(u,v) = \int_{-\infty}^{\infty}{\int_{-\infty}^{\infty}{f(x,y)e^{-j2\pi(ux,vy)}dx}dy} $

$ \color{blue} \text{and let } P_{\theta}(\rho) \text{ be the continuous-time Fourier transform of } p_{\theta}(r) \text{ given by} $
              $ \color{blue} P_{\theta}(\rho) = \int_{-\infty}^{\infty}{p_{\theta}(r)e^{-j2\pi(\rho r)}dr}. $


$ \color{blue}\text{a) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = \delta(x,y). $

$ \color{blue}\text{Solution 1:} $

$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $


$ = z \text{ when } \left\{\begin{matrix} r cos \theta - z sin \theta = 0 \\ r sin \theta + z cos \theta = 0 \end{matrix}\right. $


$ = \frac{r cos\theta}{sin \theta}, \theta > 0 $

$ {\color{red} \text{This answer is incorrect. The correct answer is as following:}} $

$ {\color{green} \text{Recall:}} $


$ {\color{green} \text{i) } \int_{-\infty}^{+\infty}{f(g(t)) \delta (t) dt} = f(g(t=0)) \int_{-\infty}^{+\infty}{\delta (t) dt} } $


$ {\color{green} \text{ii) } \int_{-\infty}^{+\infty}{\delta (\alpha t) dt} = \int_{-\infty}^{+\infty}{\delta (u) \frac{du}{|\alpha|}} = \frac{1}{|\alpha|} } $


$ {\color{green} \text{iii) } \delta() \text{ function is separable: } \delta(x,y) = \delta(x) \cdot \delta(y) } $


$ \color{green} \text{ Define } u = r cos\theta - z sin\theta $


$ \color{green} \Rightarrow dz = \frac{du}{|sin\theta|} $


$ \color{green} \text{ Now } $


$ \color{green} p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $


$ \color{green} p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(g(u)) \delta(u) \frac{du}{|sin\theta|}} = \frac{\delta(u=0)}{|sin\theta|} $


$ \color{green} = \frac{\delta(\frac{r}{sin\theta})}{|sin\theta|} = \frac{|sin\theta|}{|sin\theta|} \delta(r) = \delta(r) $

$ \color{blue}\text{Solution 2:} $

.QE 11 CS5 2 a sol2.PNG

$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $


$ = \delta(r) $


$ {\color{green} \text{Here, the student uses the intuitive solution: in this case the answer does not depend on } \theta \text{, since the image just contains a peak at origin. } } $

$ \color{blue}\text{b) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = \delta(x-1,y-1). $

$ \color{blue}\text{Solution 1:} $

$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta - 1, r sin\theta + z cos \theta - 1) dz} $

$ = z \text{ when } \left\{\begin{matrix} r cos \theta - z sin \theta = 1 \\ r sin \theta + z cos \theta = 1 \end{matrix}\right. $


$ = \frac{r cos\theta - 1}{sin \theta}, \theta > 0 $

$ {\color{red} \text{This answer is incorrect. The correct answer is as following:}} $

$ \color{green} \text{ Similar to the solution 1 to part a) we define u: } u = r cos\theta - z sin\theta - 1 $


$ \color{green} \text{ Following the same logic as in part a) we obtain the final answer:} $


$ \color{green} p_{\theta}(r) = \delta(r - (cos\theta + sin \theta)) = \delta(r - \sqrt{2} cos (\theta - \frac{\pi}{4})) $

$ \color{blue}\text{Solution 2:} $

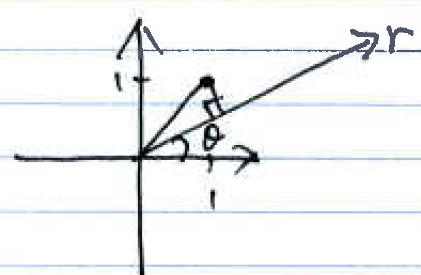
QE 11 CS5 2 b sol2.PNG

$ \tilde{p}_\theta(r) = p_{\theta}(r - \sqrt{1+1} cos(\theta - tan^{-1}(\frac{1}{1}))) $


$ = p_\theta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) $


$ = \delta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) $


$ {\color{green} \text{Again, the student uses the intuitive solution: in this case the answer does depend on } \theta \text{, since the peak is shifted from the origin to the point } (1,1). } $


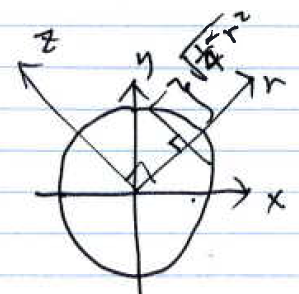
$ \color{blue}\text{c) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = rect \left(\sqrt[]{x^2+y^2} \right). $


$ \color{blue}\text{Solution 1:} $


$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{rect(\sqrt{(r cos\theta - z sin\theta)^2 + (r sin\theta + z cos \theta)^2)} dz} $


$ \color{green} \text{Recall should be added:} $

$ \color{green} rect(t) = \left\{\begin{matrix} 1, for |t|\leq \frac{1}{2} \\ 0, otherwise \end{matrix}\right. $


$ \text{therefore: } $


$ p_{\theta}(r) = \int_{-\sqrt{\frac{1}{4} - r^2}}^{\sqrt{\frac{1}{4} - r^2}}{1 dz} $


$ = \left\{\begin{matrix} \sqrt{1 - 4r^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ otherwise} \end{matrix}\right. $

$ \color{blue}\text{Solution 2:} $

QE 11 CS5 2 c sol2.PNG

$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{f(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $


$ = \int_{-\sqrt{\frac{1}{4} - r^2}}^{\sqrt{\frac{1}{4} - r^2}}{1 dz} = \sqrt{1 - 4r^2}, \text{ if }|r| \leq \frac{1}{2} $


$ \text{ else } p_{\theta}(r) = 0 $

$ \color{blue}\text{d) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = rect \left(\sqrt[]{(x-1)^2+(y-1)^2} \right). $

$ \color{blue}\text{Solution 1:} $


$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{rect \left( \sqrt{(r cos\theta - z sin\theta - 1)^2 + (r sin\theta + z cos \theta - 1)^2} \right) dz} $


$ = \int_{-\sqrt{\frac{1}{4} - (r - (cos\theta + sin\theta))^2}}^{\sqrt{\frac{1}{4} - (r - (cos\theta + sin\theta))^2}}{1 dz} $


$ = \left\{\begin{matrix} \sqrt{1 - 4(r - (cos\theta + sin\theta))^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ otherwise} \end{matrix}\right. $


$ = \left\{\begin{matrix} \sqrt{1 - 4(r - \sqrt{2} cos (\theta - \frac{\pi}{4}))^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ otherwise} \end{matrix}\right. $

$ \color{blue}\text{Solution 2:} $

$ \tilde{p}_\theta(r) = p_{\theta}(r - \sqrt{1+1} cos(\theta - tan^{-1}(\frac{1}{1}))) $


$ = p_\theta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) $


$ \text{ where } p_\theta(r) = \left\{\begin{matrix} \sqrt{1 - 4r^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ else} \end{matrix}\right. $


$ {\color{green} \text{Here, the student uses the results from solutions to part b and c.} } $

$ \color{blue}\text{e) Describe in precise detail, the steps required to perform filtered back projection (FBP) reconstruction of } f(x,y). $


$ \color{blue}\text{Solution 1:} $

$ 1. \text{ Compute } \rho_{\theta}(r) $


$ 2. \text{ Compute FT of step 1.} $

$ 3. \text{ Multiply step 2 by the filter } H(\rho) = |\rho| = f_c \left [ rect(\frac{f}{2f_c}) - \Lambda(\frac{f}{f_c}) \right ], \text{ for some cut-off, } f_c $

$ 4. \text{ Compute inverseFT of step 3; (call it) } g_\theta(r) $


$ 5. \text{ Back project } g_{\theta}(r) \text{ and get: } $

$ f(x,y) = \int_{0}^{\pi}{g_\theta(xcos\theta + ysin\theta)d\theta} $


$ { \color{green} \text{More details can be found in the below website, under Tomographic Reconstruction:} } $

https://engineering.purdue.edu/~bouman/ece637/notes/

$ \color{blue}\text{Solution 2:} $

$ 1. \text{ Measure the projections } \rho_{\theta}(r) \text{ at various angles} $

$ 2. \text{ Filter the projections } \rho_{\theta}(r) \text{ with } h(r) \text{, where } H(\rho) = |\rho| \text{ and get } g_{\theta}(r) $

$ 3. \text{ Back project } g_{\theta}(r) \text{ along } r = xcos\theta + ysin\theta \text{ and get } $

$ f(x,y) = \int_{0}^{\pi}{g_\theta(xcos\theta + ysin\theta)d\theta} $

"Communication, Networks, Signal, and Image Processing" (CS)- Question 5, August 2011

Go to

Back to ECE Qualifying Exams (QE) page

Retrieved from "https://www.projectrhea.org/rhea/index.php?title=ECE-QE_CS5-2011_solusion-2&oldid=52202"
Shortcuts
Help Main Wiki Page Random Page Special Pages Log in
Search

Alumni Liaison

Ph.D. 2007, working on developing cool imaging technologies for digital cameras, camera phones, and video surveillance cameras.

Buyue Zhang