| Line 1: | Line 1: | ||
| − | + | <br> | |
| − | =Audio Signal Generating and Processing Project= | + | = Audio Signal Generating and Processing Project = |
| − | - '''Abstract''' - | + | - '''Abstract''' - |
| − | This project is intent to analysis different musical instrument's sound, and try to create artificial musical instrument sounds to play a piece. | + | This project is intent to analysis different musical instrument's sound, and try to create artificial musical instrument sounds to play a piece. |
| − | First, by looking at the Fourier domain, one can and measure the amplitude of each harmonics. The intention is trying to produce similar amplitude harmonic cosine functions, and mix all the waveform together to construct a simulated instrument voice. | + | First, by looking at the Fourier domain, one can and measure the amplitude of each harmonics. The intention is trying to produce similar amplitude harmonic cosine functions, and mix all the waveform together to construct a simulated instrument voice. |
| − | - '''Procedure''' - | + | - '''Procedure''' - |
| − | + | :Approach 1: | |
| − | + | ||
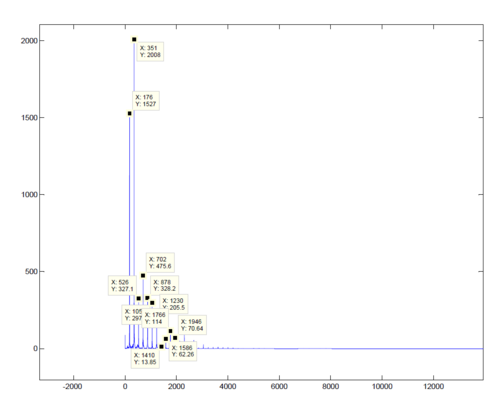
| + | ::First a couple of sound files are inspected. Particularly this | ||
| + | ::[http://www.daimi.au.dk/~jones/dsp/sounds/singlenote/Piano.ff.F3.wav single note piano sound] was used. Take the ::FFT in MATLAB, the frequency domain of the graph looks like this. | ||
| + | <br> | ||
| − | [[Image: | + | ::[[Image:Fft piano.png|500px]] |
| − | Calculating fundamental frequency: | + | ::Calculating fundamental frequency: |
| − | <math> F_{fundamental} = \frac{K|_{FFT(Data)'s 1_{st}Peak}*SampleRate}{ Number of DataPoints}</math> | + | ::<math> F_{fundamental} = \frac{K|_{FFT(Data)'s 1_{st}Peak}*SampleRate}{ Number of DataPoints}</math> |
| + | ::<br> Then one can record all the amplitude of different harmonics. Also notice that the sound amplitude is decreasing as time goes by. A decreasing exponential envelope is require for the signal to sound more like a real instrumental voice. the amplitude of the waveform of the soundtrack is 4 at very beginning, decreased to 0.5 after 1s and goes to 0.5 after 3 seconds. So an envelope function <span class="texhtml">''e''<sup>( − 2.07944154 * ''t'')</sup> = ''e''<sup>( − 2.07944154 / ''s''''a''''m''''p''''l''''e''''r''''a''''t''''e'''''<b> * ''n'')</b></sup></span> | ||
| − | + | ::Next thing need to be done, is design a pattern that plays multiple notes at the same time. The first guess is just sum up all the harmonics and get the result. But actually this doesn't work. The sound of a minor three interval sounds like this. | |
| − | + | ||
| − | the | + | |
| − | + | ||
| − | + | ::Note_A:This is a cosine function with a frequency = 440Hz. | |
| − | + | ||
| − | + | ||
| − | + | ::Namely Note_A = cos(440*2*pi*t) = cos(440*2*pi*n/Sample_Rate); | |
| − | + | ::[[Media:Audio_Signal_Generating_and_Processing_Project_FILES_Note_A.wav]] | |
| − | + | ::Note_C:This is a cosine function with a frequency = 523.251131Hz. | |
| − | + | ::Namely Note_A = cos(523.251131*2*pi*t) = cos(523.251131*2*pi*n/Sample_Rate); | |
| − | + | ::[[Media:Audio_Signal_Generating_and_Processing_Project_FILES_Note_C.wav]] | |
| − | + | ::Distorted m3 interval: this is the sum up of the Note_A and Note_C directly. | |
| − | + | ::Which sounded distorted. | |
| − | + | ::[[Media:Audio_Signal_Generating_and_Processing_Project_FILES_failed_m3_interval.wav]] | |
| − | + | <br> | |
| + | ::After some research reading online materials about mixing audios, several algorithms are tried, but a clear mix sound is still not founded. An article online mentioned that some how MATLAB doesn't allow a sound vector's amplitude to go above. As long as an coefficient less then one is multiplied to each terms, the sum of the waveform does construct a nice sound of mixed audio. | ||
| + | ::Here is a mixed C chord, consisting C,G,c,e1 four notes. | ||
| − | + | ::[[Media:Audio_Signal_Generating_and_Processing_Project_FILES_C_chord.wav]] | |
| − | + | ::As a testing, I wrote an script that plays the first two lines of Parable's piece <Canon>. | |
| − | [[Media: | + | ::[[Media:Audio_Signal_Generating_and_Processing_Project_FILES_canon_pure_frequency_with_chord.wav]] |
| − | + | <br> | |
| − | + | <br> | |
| + | ::An analysis is performed that a simulated piano voice is produced, according to the chart above. But it doesn't sound as expected. It is distorted and doesn't sound like a real piano. A better harmonic level is needed to adjust the sound. | ||
| + | ::Here is the file that contains all different harmonics. | ||
| + | ::Note that, the file contains only first harmonic, is exactly the same as the file produced by pure cosine wave. | ||
| + | ::As more harmonics added in, the sound become richer and more emotion, but not quite as the direction that is desired. Again, a better harmonic level is needed. [[Media:20111031_Simulated_Piano_sound.wav]] | ||
| − | + | ::As inspecting the contribution to non harmonic frequencies, i.e. the part on FFT plot at low frequency but not at peak looks like noise, I found that they do have significant contribution to the sound. The following method is used: Take the fft of the data, and mask off all terms that magnitude less then some level. In this case, I choose 40. So all the frequency component that less than 40 is deleted, left pure harmonic frequencies. And this sound do sound artificial and not as detailed as the original. | |
| − | + | ::So, this indicated that '''by only using integer multiples of harmonics, one can hardly simulate a very nature piano sound.''' Hence some other approach is need. | |
| − | + | <br> | |
| − | + | :Approach 2: | |
| − | + | ||
| + | ::The next reasonable idea is to modify the existing sound track to produce different pitches and length notes, then use these notes to construct a piece. | ||
| − | + | :: First Observation: | |
| − | + | :: By just playing the wav file in different sample rate can give a different pitch and duration note. | |
| + | :: As the sound sample rate goes up, pitch goes up and duration decreases. | ||
| + | :: For the region close to the original note, this is a valid approach. The note sounds nature and not distorted. | ||
| + | :: But this region only covers about up and down an octave. If go beyond this region, The sound became funny. | ||
| + | <br> | ||
| + | All Matlab files can be download here. [[Media:Audio_Signal_Generating_and_Processing_Project_FILES_MATLAB_FILES.zip]] | ||
| − | + | <br> | |
| + | [[2011 Fall ECE 438 Boutin|Back to 2011 Fall ECE 438 Boutin]] | ||
| − | + | [[Category:2011_Fall_ECE_438_Boutin]] | |
| − | + | ||
| − | [[ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Revision as of 19:18, 30 October 2011
Audio Signal Generating and Processing Project
- Abstract -
This project is intent to analysis different musical instrument's sound, and try to create artificial musical instrument sounds to play a piece.
First, by looking at the Fourier domain, one can and measure the amplitude of each harmonics. The intention is trying to produce similar amplitude harmonic cosine functions, and mix all the waveform together to construct a simulated instrument voice.
- Procedure -
- Approach 1:
- First a couple of sound files are inspected. Particularly this
- single note piano sound was used. Take the ::FFT in MATLAB, the frequency domain of the graph looks like this.
- Calculating fundamental frequency:
- $ F_{fundamental} = \frac{K|_{FFT(Data)'s 1_{st}Peak}*SampleRate}{ Number of DataPoints} $
Then one can record all the amplitude of different harmonics. Also notice that the sound amplitude is decreasing as time goes by. A decreasing exponential envelope is require for the signal to sound more like a real instrumental voice. the amplitude of the waveform of the soundtrack is 4 at very beginning, decreased to 0.5 after 1s and goes to 0.5 after 3 seconds. So an envelope function e( − 2.07944154 * t) = e( − 2.07944154 / s'a'm'p'l'e'r'a't'e * n)
- Next thing need to be done, is design a pattern that plays multiple notes at the same time. The first guess is just sum up all the harmonics and get the result. But actually this doesn't work. The sound of a minor three interval sounds like this.
- Note_A:This is a cosine function with a frequency = 440Hz.
- Namely Note_A = cos(440*2*pi*t) = cos(440*2*pi*n/Sample_Rate);
- Note_C:This is a cosine function with a frequency = 523.251131Hz.
- Namely Note_A = cos(523.251131*2*pi*t) = cos(523.251131*2*pi*n/Sample_Rate);
- Distorted m3 interval: this is the sum up of the Note_A and Note_C directly.
- Which sounded distorted.
- After some research reading online materials about mixing audios, several algorithms are tried, but a clear mix sound is still not founded. An article online mentioned that some how MATLAB doesn't allow a sound vector's amplitude to go above. As long as an coefficient less then one is multiplied to each terms, the sum of the waveform does construct a nice sound of mixed audio.
- Here is a mixed C chord, consisting C,G,c,e1 four notes.
- As a testing, I wrote an script that plays the first two lines of Parable's piece <Canon>.
- An analysis is performed that a simulated piano voice is produced, according to the chart above. But it doesn't sound as expected. It is distorted and doesn't sound like a real piano. A better harmonic level is needed to adjust the sound.
- Here is the file that contains all different harmonics.
- Note that, the file contains only first harmonic, is exactly the same as the file produced by pure cosine wave.
- As more harmonics added in, the sound become richer and more emotion, but not quite as the direction that is desired. Again, a better harmonic level is needed. Media:20111031_Simulated_Piano_sound.wav
- As inspecting the contribution to non harmonic frequencies, i.e. the part on FFT plot at low frequency but not at peak looks like noise, I found that they do have significant contribution to the sound. The following method is used: Take the fft of the data, and mask off all terms that magnitude less then some level. In this case, I choose 40. So all the frequency component that less than 40 is deleted, left pure harmonic frequencies. And this sound do sound artificial and not as detailed as the original.
- So, this indicated that by only using integer multiples of harmonics, one can hardly simulate a very nature piano sound. Hence some other approach is need.
- Approach 2:
- The next reasonable idea is to modify the existing sound track to produce different pitches and length notes, then use these notes to construct a piece.
- First Observation:
- By just playing the wav file in different sample rate can give a different pitch and duration note.
- As the sound sample rate goes up, pitch goes up and duration decreases.
- For the region close to the original note, this is a valid approach. The note sounds nature and not distorted.
- But this region only covers about up and down an octave. If go beyond this region, The sound became funny.
All Matlab files can be download here. Media:Audio_Signal_Generating_and_Processing_Project_FILES_MATLAB_FILES.zip