| Line 51: | Line 51: | ||
==Question 2== | ==Question 2== | ||
| + | a. Substituting values directly would yield the following - <br> | ||
| − | + | <math>\begin{align} | |
| + | n &= ...\text{ -3, -2, -1, 0, 1, 2, 3, 4, 5} ...\\ | ||
| + | y\left[n\right] &= ...\text{ 0, -2, -4, -1, 2, -1, -4, -2, 0} ...\\ | ||
| + | \end{align}</math> | ||
| + | b. h[n] = ? <br> Substitute x[n] = <span class="texhtml">δ[''n'']</span> to obtain y[n] = h[n], <br> h[n] = <span class="texhtml">δ[''n'']</span> + 2<span class="texhtml">δ[''n'' − 1]</span> + <span class="texhtml">δ[''n'' − 2]</span> <br> | ||
| + | |||
| + | Now x[n] = -2<span class="texhtml">δ[''n'' + 2]</span> + <span class="texhtml">δ[''n'']</span> - 2<span class="texhtml">δ[''n'' − 2]</span> <br> | ||
| + | |||
| + | <math>\begin{align} | ||
| + | y[n] &= x[n] * h[n] \\ | ||
| + | &= (-2\delta[n+2] + \delta[n] - 2\delta[n-2]) * (\delta[n] + 2\delta[n-1] + \delta[n-2]) \\ | ||
| + | &= -2\delta[n+2] - 4\delta[n+1] -2\delta[n] + \delta[n] + 2\delta[n-1] + \delta[n-2] - 2\delta[n-2] - 4\delta[n-3] - 2\delta[n-4] \\ | ||
| + | &= -2\delta[n+2] - 4\delta[n+1] - \delta[n] + 2\delta[n-1] - \delta[n-2] - 4\delta[n-3] - 2\delta[n-4] \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | c. x[n] = <span class="texhtml">''e''<sup>''j''ω''n''</sup></span> <br> (i) <br> <math>\begin{align} | ||
| + | y[n] &= e^{j\omega n} + 2 e^{j\omega (n-1)} + e^{j\omega (n-2)} \\ | ||
| + | &= e^{j\omega n}(1 + 2 e^{-j\omega } + e^{-2j\omega }) \\ | ||
| + | H(e^{j\omega}) &= 1 + 2 e^{-j\omega } + e^{-2j\omega } \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | (ii) <br> h[n] = <span class="texhtml">δ[''n'']</span> + 2<span class="texhtml">δ[''n'' − 1]</span> + <span class="texhtml">δ[''n'' − 2]</span> <br> H(<span class="texhtml">''e''<sup>''j''ω</sup></span>) = 1 + 2 <span class="texhtml">''e''<sup> − ''j''ω</sup></span> + <span class="texhtml">''e''<sup> − 2''j''ω</sup></span> <br> | ||
| + | |||
| + | (i) and (ii) are the same.<br> | ||
| + | |||
| + | d. x[n] = -2<span class="texhtml">δ[''n'' + 2]</span> + <span class="texhtml">δ[''n'']</span> - 2<span class="texhtml">δ[''n'' − 2]</span> <br> X(<span class="texhtml">''e''<sup>''j''ω</sup></span>) = -2 <span class="texhtml">''e''<sup>2''j''ω</sup></span> + 1 - 2<span class="texhtml">''e''<sup> − 2''j''ω</sup></span> <br> | ||
| + | |||
| + | <math>\begin{align} | ||
| + | Y(e^{j\omega}) &= X(e^{j\omega})H(e^{j\omega}) \\ | ||
| + | &= (-2e^{2j\omega } + 1 - 2e^{-2j\omega } ).(1 + 2e^{-j\omega } + e^{-2j\omega }) \\ | ||
| + | &= -2e^{2j\omega } - 4e^{j\omega } - 2 + 1 + 2e^{-j\omega } + 2e^{-2j\omega } - 2e^{-2j\omega } - 4e^{-3j\omega } - 2e^{-4j\omega } \\ | ||
| + | &= -2e^{2j\omega } - 4e^{j\omega } - 1 - 2e^{-j\omega } - e^{-2j\omega } - 4e^{-3j\omega } - 2e^{-4j\omega } \\ | ||
| + | \\ | ||
| + | \text{Using Inverse DTFT,} \\ | ||
| + | y[n] &= -2\delta[n+2] - 4\delta[n+1] - \delta[n] + 2\delta[n-1] - \delta[n-2] - 4\delta[n-3] - 2\delta[n-4] \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | All 3 approaches lead to the same y[n]. | ||
---- | ---- | ||
Revision as of 11:23, 29 October 2011
Contents
[hide]Homework 6, ECE438, Fall 2011, Prof. Boutin
Question 1
a)
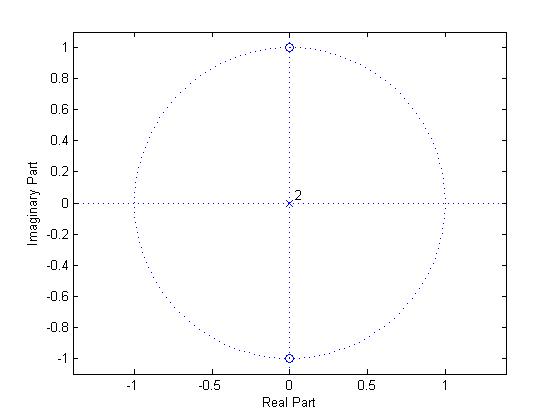
$ y[n]= \frac{x[n]+x[n-1]}{2} $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y[z]&= \frac{X[z]+X[z].z^{-1}}{2} \\ \frac{Y[z]}{X[z]}&= \frac{1+z^{-1}}{2} \\ H[z] &= \frac{1+z^{-1}}{2} \\ \end{align} $
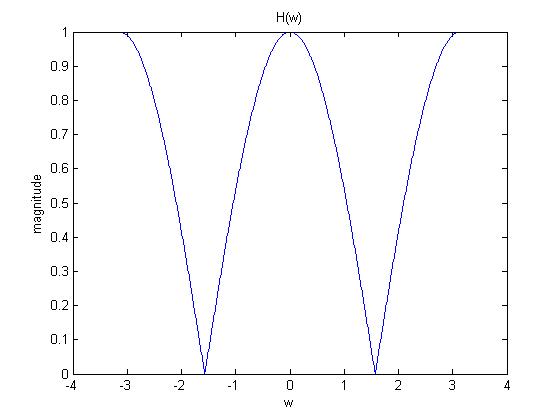
Frequency Response $ H(\omega) $
$ \begin{align} H[e^{j\omega }] &= \frac{1+e^{-j\omega }}{2} \\ &= e^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}+e^{-j\frac{\omega }{2}}}{2} \right) \\ &= e^{-j\frac{\omega }{2}} cos \left( \frac{\omega }{2} \right) \\ \end{align} $
b)
$ y[n]= \frac{x[n]-x[n-1]}{2} $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y[z]&= \frac{X[z]-X[z].z^{-1}}{2} \\ \frac{Y_2[z]}{X[z]}&= \frac{1-z^{-1}}{2} \\ H[z] &= \frac{1-z^{-1}}{2} \\ \end{align} $
Frequency Response $ H(\omega) $
$ \begin{align} H[e^{j\omega }] &= \frac{1-e^{-j\omega }}{2} \\ &= e^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}-e^{-j\frac{\omega }{2}}}{2} \right) \\ &= je^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}-e^{-j\frac{\omega }{2}}}{2j} \right) \\ &= je^{-j\frac{\omega }{2}} sin \left( \frac{\omega }{2} \right) \\ \end{align} $
Question 2
a. Substituting values directly would yield the following -
$ \begin{align} n &= ...\text{ -3, -2, -1, 0, 1, 2, 3, 4, 5} ...\\ y\left[n\right] &= ...\text{ 0, -2, -4, -1, 2, -1, -4, -2, 0} ...\\ \end{align} $
b. h[n] = ?
Substitute x[n] = δ[n] to obtain y[n] = h[n],
h[n] = δ[n] + 2δ[n − 1] + δ[n − 2]
Now x[n] = -2δ[n + 2] + δ[n] - 2δ[n − 2]
$ \begin{align} y[n] &= x[n] * h[n] \\ &= (-2\delta[n+2] + \delta[n] - 2\delta[n-2]) * (\delta[n] + 2\delta[n-1] + \delta[n-2]) \\ &= -2\delta[n+2] - 4\delta[n+1] -2\delta[n] + \delta[n] + 2\delta[n-1] + \delta[n-2] - 2\delta[n-2] - 4\delta[n-3] - 2\delta[n-4] \\ &= -2\delta[n+2] - 4\delta[n+1] - \delta[n] + 2\delta[n-1] - \delta[n-2] - 4\delta[n-3] - 2\delta[n-4] \\ \end{align} $
c. x[n] = ejωn
(i)
$ \begin{align} y[n] &= e^{j\omega n} + 2 e^{j\omega (n-1)} + e^{j\omega (n-2)} \\ &= e^{j\omega n}(1 + 2 e^{-j\omega } + e^{-2j\omega }) \\ H(e^{j\omega}) &= 1 + 2 e^{-j\omega } + e^{-2j\omega } \\ \end{align} $
(ii)
h[n] = δ[n] + 2δ[n − 1] + δ[n − 2]
H(ejω) = 1 + 2 e − jω + e − 2jω
(i) and (ii) are the same.
d. x[n] = -2δ[n + 2] + δ[n] - 2δ[n − 2]
X(ejω) = -2 e2jω + 1 - 2e − 2jω
$ \begin{align} Y(e^{j\omega}) &= X(e^{j\omega})H(e^{j\omega}) \\ &= (-2e^{2j\omega } + 1 - 2e^{-2j\omega } ).(1 + 2e^{-j\omega } + e^{-2j\omega }) \\ &= -2e^{2j\omega } - 4e^{j\omega } - 2 + 1 + 2e^{-j\omega } + 2e^{-2j\omega } - 2e^{-2j\omega } - 4e^{-3j\omega } - 2e^{-4j\omega } \\ &= -2e^{2j\omega } - 4e^{j\omega } - 1 - 2e^{-j\omega } - e^{-2j\omega } - 4e^{-3j\omega } - 2e^{-4j\omega } \\ \\ \text{Using Inverse DTFT,} \\ y[n] &= -2\delta[n+2] - 4\delta[n+1] - \delta[n] + 2\delta[n-1] - \delta[n-2] - 4\delta[n-3] - 2\delta[n-4] \\ \end{align} $
All 3 approaches lead to the same y[n].
Question 3
Question 4
Question 5
Back to Homework 6
Back to ECE 438 Fall 2011