| Line 4: | Line 4: | ||
==Question 1== | ==Question 1== | ||
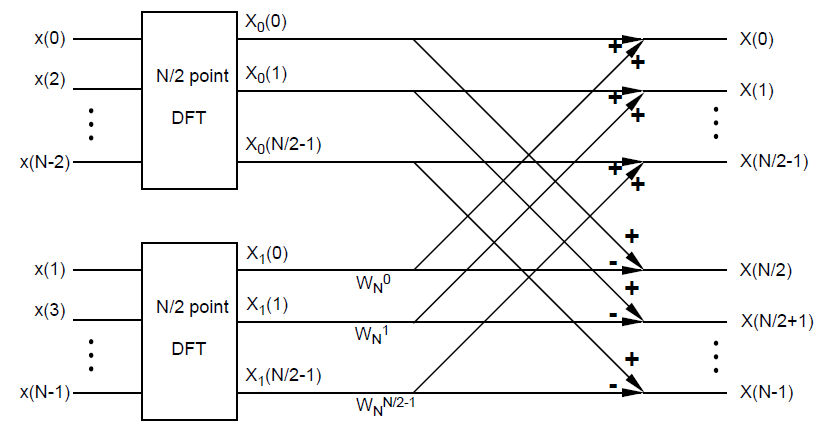
| − | Diagram of "decimation by two" FFT computing | + | Diagram of "decimation by two" FFT computing N-pt DFT. N=8 in this question. |
[[Image:HW5Q1fig1.jpg]] | [[Image:HW5Q1fig1.jpg]] | ||
| − | where <math>W_N^k = e^{-j2\pi k/N} | + | where <math>W_N^k = e^{-j2\pi k/N}</math> |
Recall the definition of DFT: | Recall the definition of DFT: | ||
| Line 16: | Line 16: | ||
For each k, we need N times complex multiplications and N-1 times complex additions. | For each k, we need N times complex multiplications and N-1 times complex additions. | ||
| − | In total, we need <math>N^2</math> times of complex multiplications and <math>N^2-N</math> times of complex additions. | + | In total, we need <math>N^2 = 64</math> times of complex multiplications and <math>N^2-N = 56</math> times of complex additions. |
| − | + | Using "decimation by two" FFT algorithm, the DFT is computed in two steps. For the first step, two N/2-pt DFT are computed with <math>2\cdot (\frac{N}{2})^2</math> multiplications and <math>2((\frac{N}{2})^2-\frac{N}{2})</math>. For the second step, <math>\frac{N}{2}</math> multiplications and <math>N</math> additions are needed. | |
When <math>N=8</math>, the total numbers of complex operations are | When <math>N=8</math>, the total numbers of complex operations are | ||
| Line 32: | Line 32: | ||
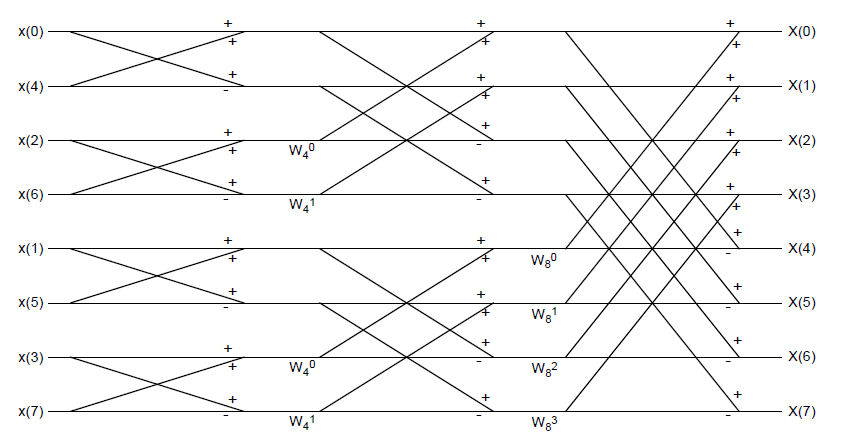
[[Image:HW5Q2fig1.jpg]] | [[Image:HW5Q2fig1.jpg]] | ||
| + | |||
| + | where <math>W_N^k = e^{-j2\pi k/N}</math> | ||
Recall the definition of DFT: | Recall the definition of DFT: | ||
| Line 52: | Line 54: | ||
==Question 3== | ==Question 3== | ||
| + | The diagram is identical to the diagram in Question 1 except N=122. | ||
| + | |||
| + | By similar argument presented in Question 1, a direct computation of DFT requires <math>N^2 = 14884</math> times of complex multiplications and <math>N^2-N = 14762</math> times of complex additions. | ||
| + | Using "decimation by two" FFT algorithm, the total number of multiplications is <math>2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 7503</math> and the total number of additions is <math>2((\frac{N}{2})^2-\frac{N}{2}) + N = 7442</math> | ||
---- | ---- | ||
Revision as of 15:31, 23 October 2011
Homework 5, ECE438, Fall 2011, Prof. Boutin
Question 1
Diagram of "decimation by two" FFT computing N-pt DFT. N=8 in this question.
where $ W_N^k = e^{-j2\pi k/N} $
Recall the definition of DFT:
$ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1 $.
For each k, we need N times complex multiplications and N-1 times complex additions.
In total, we need $ N^2 = 64 $ times of complex multiplications and $ N^2-N = 56 $ times of complex additions.
Using "decimation by two" FFT algorithm, the DFT is computed in two steps. For the first step, two N/2-pt DFT are computed with $ 2\cdot (\frac{N}{2})^2 $ multiplications and $ 2((\frac{N}{2})^2-\frac{N}{2}) $. For the second step, $ \frac{N}{2} $ multiplications and $ N $ additions are needed.
When $ N=8 $, the total numbers of complex operations are
multiplications: $ 2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 36 $
additions: $ 2((\frac{N}{2})^2-\frac{N}{2}) + N = 32 $
Question 2
Diagram of "radix-2" FFT computing 8-pt DFT.
where $ W_N^k = e^{-j2\pi k/N} $
Recall the definition of DFT:
$ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1 $
In this question N=8
If we use summation formula to compute DFT, for each k, we need N times complex multiplications and N-1 times complex additions.
In total, we need N*N=64 times of complex multiplications and N*(N-1)=56 times of complex additions.
In decimation-in-time FFT algorithm, we keep on decimating the number of points by 2 until we get 2 points DFT. At most, we can decimate $ v=log_2 N $ times. As a result, we get v levels of DFT. Except for the first level (2-pt FFT), which only needs N times complex additions, for the rest of levels, we need N/2 times of complex multiplications and N times of complex additions.
In total, we need $ \frac{N}{2}(log_2 N -1)=8 $ times of complex multiplications and $ Nlog_2 N=24 $ times of complex additions.
(Note: when $ N $ is large, $ log_2 N -1 \approx log_2 N $. So the number of multiplications becomes $ \frac{N}{2}log_2 N $.)
Question 3
The diagram is identical to the diagram in Question 1 except N=122.
By similar argument presented in Question 1, a direct computation of DFT requires $ N^2 = 14884 $ times of complex multiplications and $ N^2-N = 14762 $ times of complex additions.
Using "decimation by two" FFT algorithm, the total number of multiplications is $ 2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 7503 $ and the total number of additions is $ 2((\frac{N}{2})^2-\frac{N}{2}) + N = 7442 $
Back to Homework 5
Back to ECE 438 Fall 2011