| Line 10: | Line 10: | ||
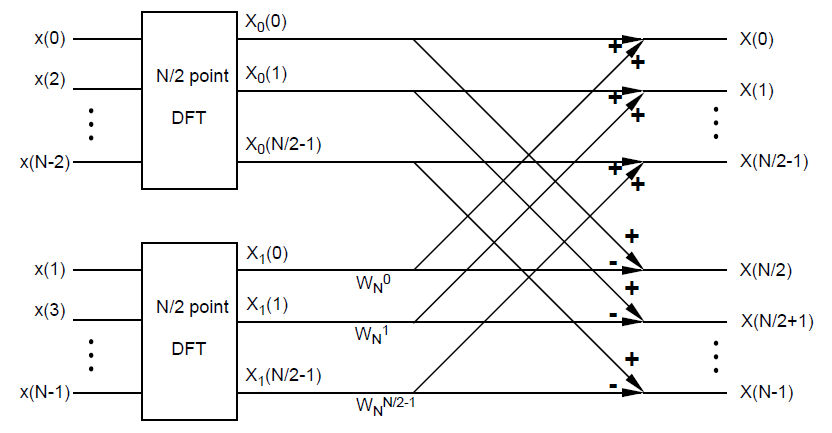
where <math>W_N^k = e^{-j2\pi k/N},\ N=8</math> | where <math>W_N^k = e^{-j2\pi k/N},\ N=8</math> | ||
| + | Recall the definition of DFT: | ||
| + | |||
| + | <math>X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1</math>. | ||
| + | |||
| + | For each k, we need N times complex multiplications and N-1 times complex additions. | ||
| + | |||
| + | In total, we need <math>N^2</math> times of complex multiplications and <math>N^2-N</math> times of complex additions. | ||
| + | |||
| + | In this algorithm, the DFT is computed in two steps. For the first step, two N/2-pt DFT are computed with <math>2\cdot (\frac{N}{2})^2</math> multiplications and <math>2((\frac{N}{2})^2-\frac{N}{2})</math>. For the second step, <math>\frac{N}{2}</math> multiplications and <math>N</math> additions are needed. | ||
| + | |||
| + | When <math>N=8</math>, the total numbers of complex operations are | ||
| + | |||
| + | multiplications: <math>2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 36</math> | ||
| + | additions: <math>2((\frac{N}{2})^2-\frac{N}{2}) + N = 32</math> | ||
---- | ---- | ||
| Line 21: | Line 35: | ||
Recall the definition of DFT: | Recall the definition of DFT: | ||
| − | <math>X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N}</math> | + | <math>X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1</math> |
In this question N=8 | In this question N=8 | ||
Revision as of 15:17, 23 October 2011
Homework 5, ECE438, Fall 2011, Prof. Boutin
Question 1
Diagram of "decimation by two" FFT computing 8-pt DFT.
where $ W_N^k = e^{-j2\pi k/N},\ N=8 $
Recall the definition of DFT:
$ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1 $.
For each k, we need N times complex multiplications and N-1 times complex additions.
In total, we need $ N^2 $ times of complex multiplications and $ N^2-N $ times of complex additions.
In this algorithm, the DFT is computed in two steps. For the first step, two N/2-pt DFT are computed with $ 2\cdot (\frac{N}{2})^2 $ multiplications and $ 2((\frac{N}{2})^2-\frac{N}{2}) $. For the second step, $ \frac{N}{2} $ multiplications and $ N $ additions are needed.
When $ N=8 $, the total numbers of complex operations are
multiplications: $ 2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 36 $
additions: $ 2((\frac{N}{2})^2-\frac{N}{2}) + N = 32 $
Question 2
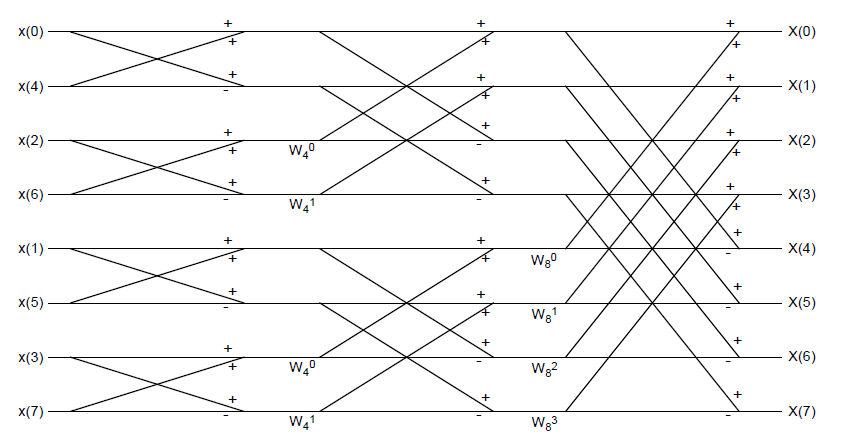
Diagram of "radix-2" FFT computing 8-pt DFT.
Recall the definition of DFT:
$ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1 $
In this question N=8
If we use summation formula to compute DFT, for each k, we need N times complex multiplications and N-1 times complex additions.
In total, we need N*N=64 times of complex multiplications and N*(N-1)=56 times of complex additions.
In decimation-in-time FFT algorithm, we keep on decimating the number of points by 2 until we get 2 points DFT. At most, we can decimate $ v=log_2 N $ times. As a result, we get v levels of DFT. Except for the first level (2-pt FFT), which only needs N times complex additions, for the rest of levels, we need N/2 times of complex multiplications and N times of complex additions.
In total, we need $ \frac{N}{2}(log_2 N -1)=8 $ times of complex multiplications and $ Nlog_2 N=24 $ times of complex additions.
(Note: when $ N $ is large, $ log_2 N -1 \approx log_2 N $. So the number of multiplications becomes $ \frac{N}{2}log_2 N $.)
Question 3
Back to Homework 5
Back to ECE 438 Fall 2011