| Line 47: | Line 47: | ||
<math>\begin{align} | <math>\begin{align} | ||
X_d(\omega)=DTFT\{ x[n] \} &= X_s(\frac{\omega}{2\pi T}) \\ | X_d(\omega)=DTFT\{ x[n] \} &= X_s(\frac{\omega}{2\pi T}) \\ | ||
| − | &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}X(\frac{\omega}{2\pi T}-\frac{5Wk}{2\pi}) | + | &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}X(\frac{\omega}{2\pi T}-\frac{5Wk}{2\pi}) \\ |
| + | &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}X(\frac{5W}{2\pi}(\frac{\omega}{2\pi}-k)) | ||
\end{align}</math> | \end{align}</math> | ||
| + | |||
| + | [[Image:HW3Q1fig3.jpg|1000px]] | ||
---- | ---- | ||
Revision as of 10:16, 15 October 2011
Homework 1, ECE438, Fall 2011, Prof. Boutin
Question 1-5
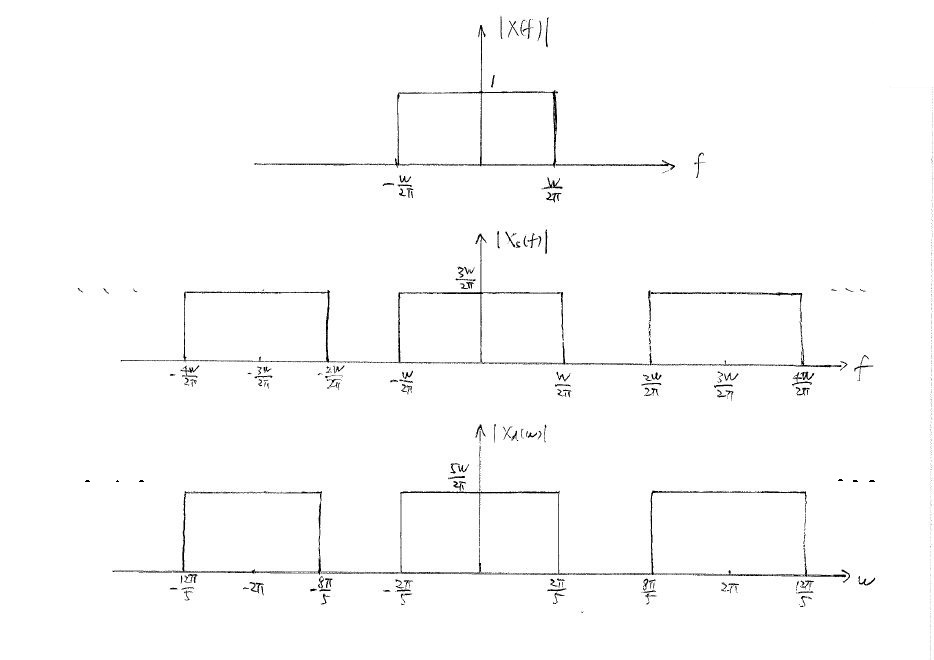
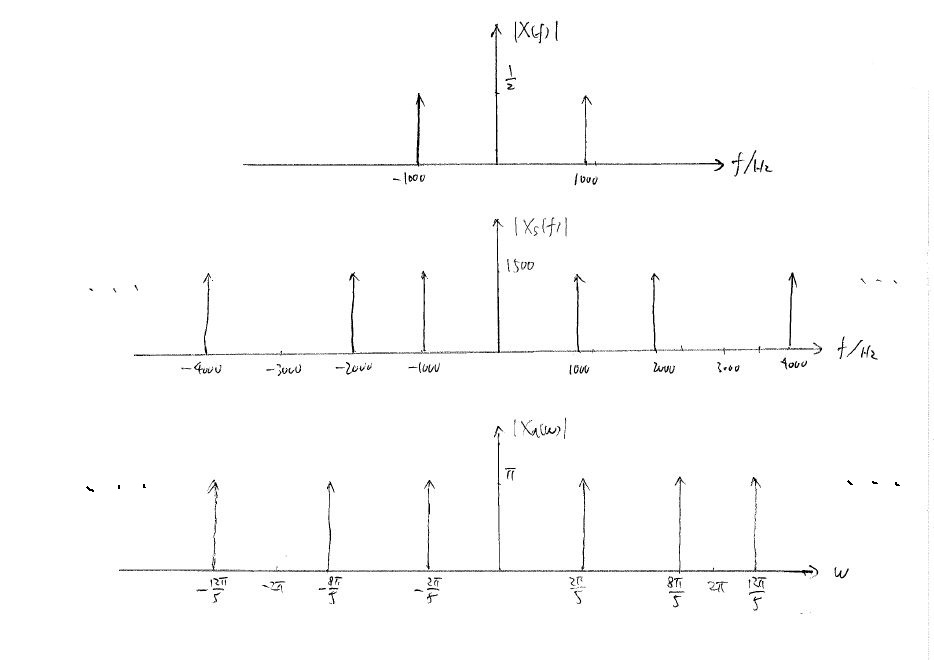
(1) $ x(t)=\frac{sin(Wt)}{\pi t} $
a) Compute CTFT of $ x(t) $. Instead of using CTFT formula, we solve it by using inverse CTFT and comparison.
$ \begin{align} x(t) &= \frac{sin(Wt)}{\pi t} = \frac{e^{jWt}-e^{-jWt}}{2j\pi t}\ (*)\\ x(t) &= \int\limits_{-\infty}^{\infty}X(f)e^{j2\pi ft}df\ (**) \end{align} $
Since
$ \int\limits_{-\frac{W}{2\pi}}^{\frac{W}{2\pi}}1\cdot e^{j2\pi ft}df = \frac{e^{jWt}-e^{-jWt}}{2j\pi t} $
Therefore,
$ X(f) = rect(\frac{\pi f}{W}) = \left\{\begin{array}{ll}1, & \text{ if }|t|<\frac{W}{2\pi},\\ 0, & \text{else.}\end{array} \right. \ $
b) the Nyquist rate
$ f_0=\frac{W}{2\pi} $
c)
$ T=\frac{1}{3f_0}=\frac{2\pi}{3W} $
$ x_s(t) = comb_T(x(t)) = x(t)\sum_{k=-\infty}^{\infty}\delta(t-kT) $
$ \begin{align} X_s(f) = CTFT\{ x_s(t) \} &= X(f)*\frac{1}{T}\sum_{k=-\infty}^{\infty}\delta(f-\frac{k}{T}) \\ &= \frac{1}{T}\sum_{k=-\infty}^{\infty}X(f-\frac{k}{T}) \\ &= \frac{3W}{2\pi}\sum_{k=-\infty}^{\infty}X(f-\frac{3Wk}{2\pi}) \end{align} $
d)
$ T=\frac{1}{5f_0}=\frac{2\pi}{5W} $
$ \begin{align} X_d(\omega)=DTFT\{ x[n] \} &= X_s(\frac{\omega}{2\pi T}) \\ &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}X(\frac{\omega}{2\pi T}-\frac{5Wk}{2\pi}) \\ &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}X(\frac{5W}{2\pi}(\frac{\omega}{2\pi}-k)) \end{align} $
Question 6
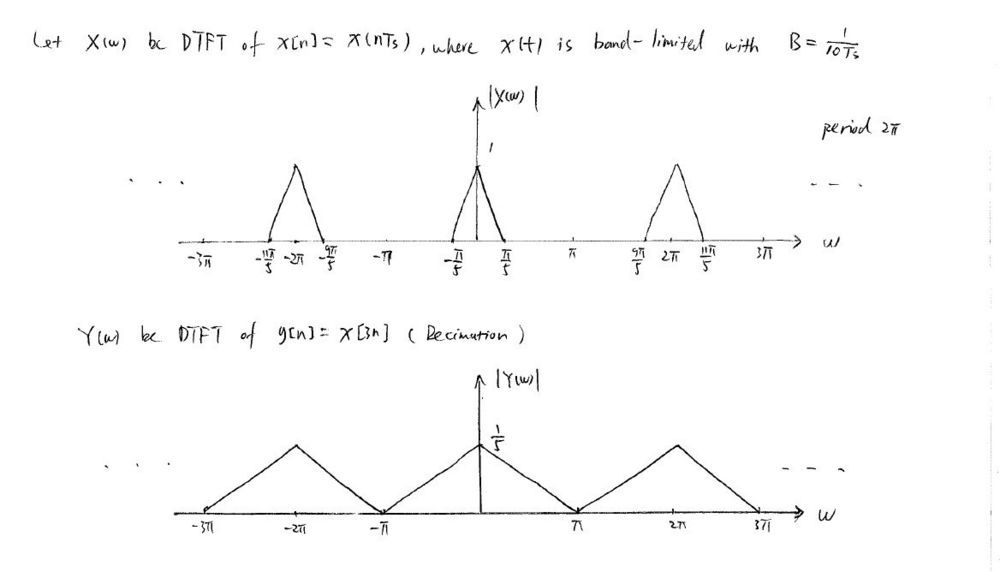
$ \text{a)} \;\; \text{General Relation for the decimation with a factor of } D \,\! $.
$ \text{Let } X(w) = \mathcal{F}(x[n]) $
$ \begin{align} Y(w) &= \sum_{n=-\infty}^{\infty} y[n]e^{-jwn} = \sum_{n=-\infty}^{\infty} x[3n]e^{-jwn} \\ &= \sum_{m=-\infty, m=Dk}^{\infty} x[m]e^{-j\frac{wm}{D}} = \sum_{m=-\infty}^{\infty} x[m] \left( \sum_{k=-\infty}^{\infty} \delta[m-Dk] \right) e^{-j\frac{wm}{D}} \\ &= \sum_{m=-\infty}^{\infty} x[m] \left( \frac{1}{D} \sum_{k=0}^{D-1} e^{j\frac{2\pi}{D}km} \right) e^{-j\frac{wm}{D}} = \sum_{k=0}^{D-1} \frac{1}{D} \sum_{m=-\infty}^{\infty} x[m]e^{j\left(w-\frac{2\pi}{D}k\right)m} \\ &= \sum_{k=0}^{D-1} \frac{1}{D} X\left(\frac{w-2\pi k}{D}\right) \\ \end{align} $
Replacing D with 5 would be the answer.
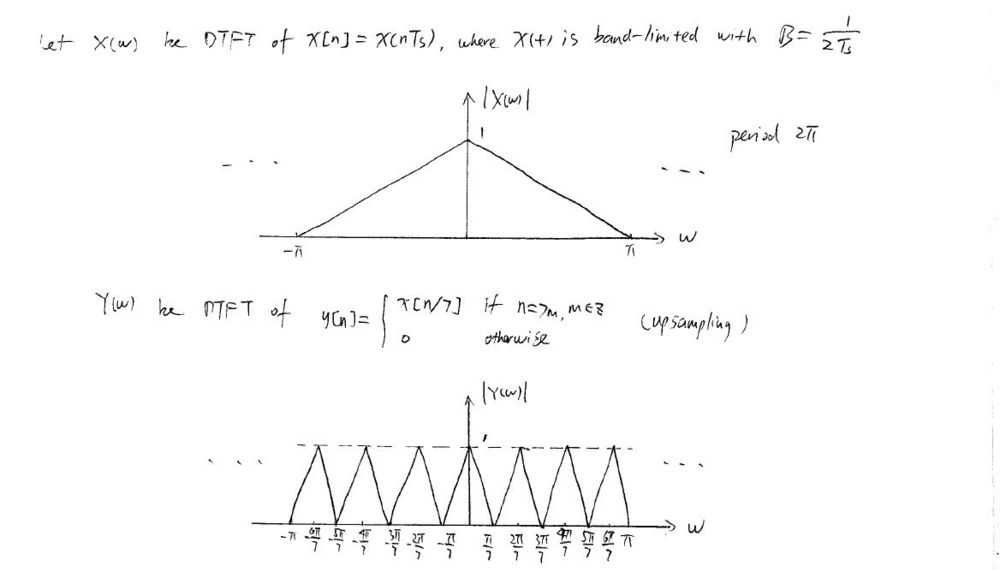
$ \text{b)} \;\; \text{General Relation for the upsampling with a factor of } L \,\! $.
$ \begin{align} Z(w) &= \sum_{n=-\infty}^{\infty} z[n]e^{-jwn} \\ &= \sum_{n=-\infty}^{\infty} \left( \sum_{k=-\infty}^{\infty} x[k] \delta[n-kL] \right) e^{-jwn} \\ &= \sum_{k=-\infty}^{\infty} x[k] \sum_{n=-\infty}^{\infty} \delta[n-kL] e^{-jwn} = \sum_{k=-\infty}^{\infty} x[k] e^{-jwkL} \\ &= \sum_{k=-\infty}^{\infty} x[k] e^{-jLwk} = X(Lw) \\ &\end{align} $
Since $ X(w) $ is periodic with $ 2\pi $, $ Z(w)=X(Lw) $ is periodic with $ 2\pi/L $.
Replaing L with 7 would be the answer.
Back to Homework 3
Back to ECE 438 Fall 2011