| Line 21: | Line 21: | ||
Also notice that the sound amplitude is decreasing as time goes by. A decreasing exponential envelope is require for the signal to sound more like a real instrumental voice. | Also notice that the sound amplitude is decreasing as time goes by. A decreasing exponential envelope is require for the signal to sound more like a real instrumental voice. | ||
the amplitude of the waveform of the soundtrack is 4 at very beginning, decreased to 0.5 after 1s and goes to 0.5 after 3 seconds. So an envelope function | the amplitude of the waveform of the soundtrack is 4 at very beginning, decreased to 0.5 after 1s and goes to 0.5 after 3 seconds. So an envelope function | ||
| − | <math> e^(-2.07944154*t) = e^(-2.07944154/samplerate*n) </math> | + | <math> e^{(-2.07944154*t)} = e^{(-2.07944154/samplerate*n)} </math> |
Next thing need to be done, is design a pattern that plays multiple notes at the same time. | Next thing need to be done, is design a pattern that plays multiple notes at the same time. | ||
Revision as of 16:34, 28 September 2011
Audio Signal Generating and Processing Project
- Abstract -
This project is intent to analysis different musical instrument's sound, and try to create artificial musical instrument sounds to play a piece.
First, by looking at the Fourier domain, one can and measure the amplitude of each harmonics. The intention is trying to produce similar amplitude harmonic cosine functions, and mix all the waveform together to construct a simulated instrument voice.
- Procedure -
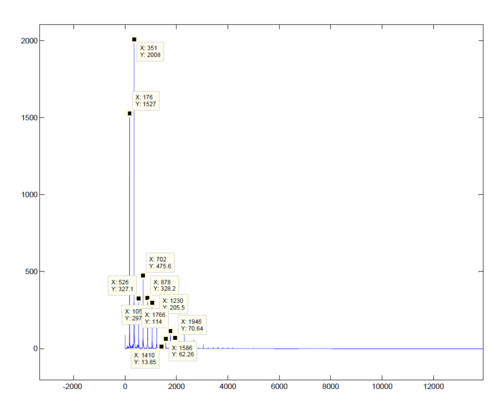
First a couple of sound files are inspected. Particularly this single note piano sound was used. Take the FFT in MATLAB, the frequency domain of the graph looks like this.
Then one can record all the amplitude of different harmonics. Also notice that the sound amplitude is decreasing as time goes by. A decreasing exponential envelope is require for the signal to sound more like a real instrumental voice. the amplitude of the waveform of the soundtrack is 4 at very beginning, decreased to 0.5 after 1s and goes to 0.5 after 3 seconds. So an envelope function $ e^{(-2.07944154*t)} = e^{(-2.07944154/samplerate*n)} $
Next thing need to be done, is design a pattern that plays multiple notes at the same time. The first guess is just sum up all the harmonics and get the result. But actually this doesn't work. The sound of a minor three interval sounds like this.
Note_A:
Media:Audio_Signal_Generating_and_Processing_Project_FILES_Note_A.wav
Note_C:
Media:Audio_Signal_Generating_and_Processing_Project_FILES_Note_C.wav
Distorted m3 interval.
Media:Audio_Signal_Generating_and_Processing_Project_FILES_failed_m3_interval.wav
After some research reading online materials about mixing audios, several algorithms are tried, but a clear mix sound is still not founded. An article online mentioned that some how MATLAB doesn't allow a sound vector's amplitude to go above. As long as an coefficient less then one is multiplied to each terms, the sum of the waveform do construct a nice sound of mixed audio.