| Line 29: | Line 29: | ||
== Applications == | == Applications == | ||
| − | Linearity can be used simplify the Fourier transform. Integration and differentiation are also linear. Once a non-linear system is made linear, complex systems are easier to model mathematically. True linear systems are virtually unknown in the real world, but over a small range of variables, systems can be modeled as linear. | + | Linearity can be used to simplify the Fourier transform. Integration and differentiation are also linear. Once a non-linear system is made linear, complex systems are easier to model mathematically. True linear systems are virtually unknown in the real world, but over a small range of variables, systems can be modeled as linear. |
<br> | <br> | ||
Revision as of 10:47, 6 May 2011
Linearity
Theory
There are three definitions we discussed in class for linearity.
Definition 1
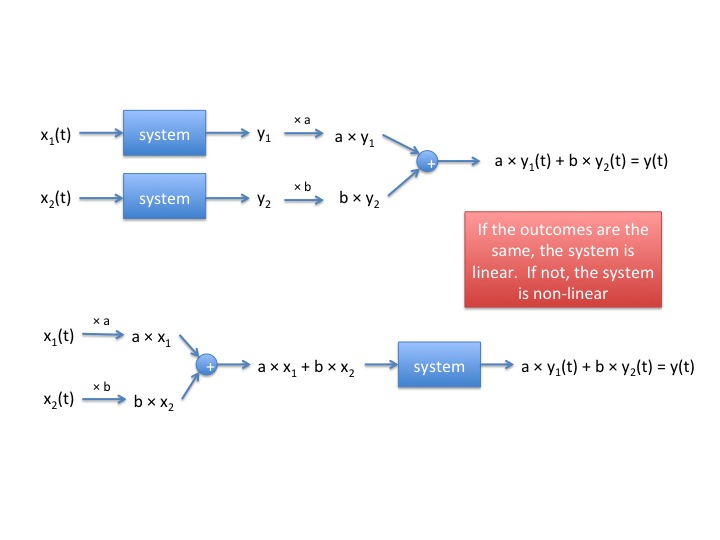
A system is called linear if for any constants $ a,b\in $ all complex numbers and for any input signals x1(t),x2(t) with response y1(t),y2(t), respectively, the system's response to ax1(t) + bx2(t) is ay1(t) + by2(t).
Definition 2
If
$ x_1(t) \rightarrow \begin{bmatrix} system \end{bmatrix} \rightarrow y_1(t) $
$ x_2(t) \rightarrow \begin{bmatrix} system \end{bmatrix} \rightarrow y_2(t) $
then
$ ax_1(t) + bx_2(t) \rightarrow \begin{bmatrix} system \end{bmatrix} \rightarrow ay_1(t) + by_2(t) $
for any $ a,b\in $ all complex numbers, any x1(t),x2(t) then we say the system is linear.
Definition 3
Applications
Linearity can be used to simplify the Fourier transform. Integration and differentiation are also linear. Once a non-linear system is made linear, complex systems are easier to model mathematically. True linear systems are virtually unknown in the real world, but over a small range of variables, systems can be modeled as linear.