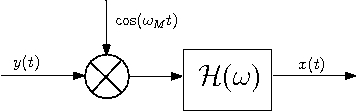| Line 27: | Line 27: | ||
:<math>\omega_c>1000\pi</math> | :<math>\omega_c>1000\pi</math> | ||
| − | d)In order to recover signal <math>x(t)</math> we multiply <math>y_2(t)</math> by <math>\sin(\omega_c t)</math> first. The signal after multiplying with <math>\sin(\omega_c t)</math> is: | + | d) In order to recover signal <math>x(t)</math> we multiply <math>y_2(t)</math> by <math>\sin(\omega_c t)</math> first. The signal after multiplying with <math>\sin(\omega_c t)</math> is: |
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 36: | Line 36: | ||
</math> | </math> | ||
| − | Thus in order to recover <math>x(t)</math> we need to filter out the second term of <math>r(t)</math> and amplify the remainder by a factor of 2 (you may want to draw the FT of <math>r(t)</math> to verify this). To achieve that, we pass <math>r(t)</math> through a low pass filter with a cut-off frequency <math>\omega_{cut}=\omega_M=1000\pi</math> and gain 2. The frequency response of this low pass filter is: | + | Thus in order to recover <math>x(t)</math> we need to filter out the second term of <math>r(t)</math> and amplify the remainder by a factor of 2 (you may want to draw the FT of <math>r(t)</math> to verify this in the frequency domain). To achieve that, we pass <math>r(t)</math> through a low pass filter with a cut-off frequency <math>\omega_{cut}=\omega_M=1000\pi</math> and gain 2. The frequency response of this low pass filter is: |
:<math>\mathcal{H}(\omega)=\left\{\begin{array}{ll} | :<math>\mathcal{H}(\omega)=\left\{\begin{array}{ll} | ||
| Line 110: | Line 110: | ||
where <math class="inline">\mathcal{H}(\omega)=\left\{\begin{array}{ll} | where <math class="inline">\mathcal{H}(\omega)=\left\{\begin{array}{ll} | ||
| − | + | 1, & \mbox{ for } |\omega|<\omega_M\\ | |
0, & \mbox{ elsewhere} | 0, & \mbox{ elsewhere} | ||
\end{array}\right. | \end{array}\right. | ||
</math>. | </math>. | ||
| − | Note that <math>\mathcal{H}(\omega)</math> is the frequency response of a low pass filter with cut-off frequency equals to <math>\omega_M</math>. | + | Note that <math class="inline">\mathcal{H}(\omega)</math> is the frequency response of a low pass filter with cut-off frequency equals to <math>\omega_M</math>. |
Revision as of 07:07, 14 April 2011
Contents
Homework 10 Solutions, ECE301 Spring 2011 Prof. Boutin
Students should feel free to make comments/corrections or ask questions directly on this page.
Question 1
a) We can write
- $ y_1(t)=e^{j \theta_c}x(t)e^{j\omega_c t} $
Notice that this is exactly as modulating by $ e^{j\omega_c t} $ but now we are multiplying with a complex exponential independent of $ t $ (phase shift). We can recover the signal $ x(t) $ for any $ \omega_c $, and hence there are no conditions put on $ \omega_c $.
b) In order to recover signal $ x(t) $, we multiply $ y_1(t) $ by $ e^{-j(\omega_c+\theta_c)} $.
c) We can write
- $ y_2(t)=x(t)\left(\frac{e^{j\omega_c t}-e^{-j\omega_c t}}{2j}\right) $
Taking the FT of $ y_2(t) $, we get:
- $ \begin{align} \mathcal{Y}_2(\omega)&=\frac{1}{2\pi(2j)}\mathcal{X}(\omega)*[2\pi\delta(\omega-\omega_c)-2\pi\delta(\omega+\omega_c)] \\ &=\frac{1}{2j}\mathcal{X}(\omega-\omega_c)-\frac{1}{2j}\mathcal{X}(\omega+\omega_c) \end{align} $
Now, to insure that we can recover signal $ x(t) $ we need to avoid having the two images of $ X(\omega) $ overlap. Hence we need $ \omega_c>\omega_M $. But $ \omega_M=2000\pi/2=1000\pi $. Hence in order for $ x(t) $ to be recoverable we need:
- $ \omega_c>1000\pi $
d) In order to recover signal $ x(t) $ we multiply $ y_2(t) $ by $ \sin(\omega_c t) $ first. The signal after multiplying with $ \sin(\omega_c t) $ is:
- $ \begin{align} r(t)&=y_2(t)\sin(\omega_c t) \\ &=\sin^2(\omega_c t)x(t) \\ &=\frac{1}{2}x(t)-\frac{1}{2}\cos(2\omega_c t)x(t) \end{align} $
Thus in order to recover $ x(t) $ we need to filter out the second term of $ r(t) $ and amplify the remainder by a factor of 2 (you may want to draw the FT of $ r(t) $ to verify this in the frequency domain). To achieve that, we pass $ r(t) $ through a low pass filter with a cut-off frequency $ \omega_{cut}=\omega_M=1000\pi $ and gain 2. The frequency response of this low pass filter is:
- $ \mathcal{H}(\omega)=\left\{\begin{array}{ll} 2, & \mbox{ for } |\omega|<1000\pi\\ 0, & \mbox{ elsewhere} \end{array}\right. $
Note that the cut-off frequency of the low pass filter can actually be anywhere between $ \omega_M $ and $ 2\omega_c-\omega_M $.
Question 2
a) The Fourier series coefficients of $ c(t) $ are:
- $ \begin{align} a_k&=\frac{\sin(\frac{2\pi k 10^{-3}}{4\times 10^{-3}})}{\pi k} \\ &=\frac{\sin{\frac{\pi k}{2}}}{\pi k} \end{align} $
and using the synthesis equation of the Fourier series we get:
- $ c(t)=\sum_{k=-\infty}^{\infty} a_k e^{j\frac{2\pi k}{T}t}=\sum_{k=-\infty}^{\infty} a_k e^{j2000\pi kt} $
Taking the FT of the latter sum, we get:
- $ \mathcal{C}(\omega)=2\pi\sum_{k=-\infty}^{\infty}a_k \delta(\omega-2000\pi k) $
Now, let $ y(t)=x(t)c(t) $, then:
$ \begin{align} \mathcal{Y}(\omega)&=\frac{1}{2\pi}\mathcal{X}(\omega)*\mathcal{C}(\omega) \\ &=\frac{1}{2\pi}\mathcal{X}(\omega)*2\pi\sum_{k=-\infty}^{\infty}a_k \delta(\omega-2000\pi k) \\ &=\sum_{k=-\infty}^{\infty}a_k \mathcal{X}(\omega-2000\pi k) \end{align} $
In order to recover $ x(t) $ we need to avoid aliasing and hence $ 2000\pi>2\omega_M $. Then $ \omega_M<1000\pi $.
b) We need to find $ a_0 $ since the image at DC is multiplied by it:
- $ a_0=\lim_{k\to 0}\frac{\sin{\frac{\pi k}{2}}}{\pi k}=\frac{\frac{\pi k}{2}}{\pi k}=\frac{1}{2} $
Now, to recover $ x(t) $ we need to filter out the images other than the image at DC and and multiply it by $ \frac{1}{a_0}=2 $. Hence we use a low pass filter with the following frequency response:
- $ \mathcal{H}(\omega)=\left\{\begin{array}{ll} 2, & \mbox{ for } |\omega|<\omega_{M}\\ 0, & \mbox{ elsewhere} \end{array}\right. $
Note that the cut-off frequency of the low pass filter can actually be anywhere between $ \omega_M $ and $ 2000\pi-\omega_M $.
Question 3
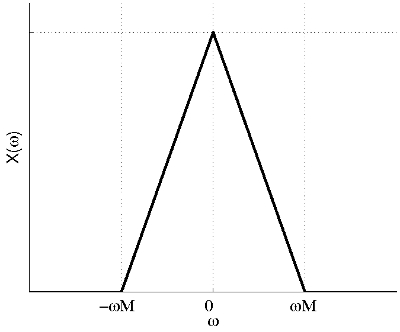
a) We can assume any illustrative shape for the spectrum of signal $ x(t) $ as long as it is band-limited between $ -\omega_M $ and $ \omega_M $.
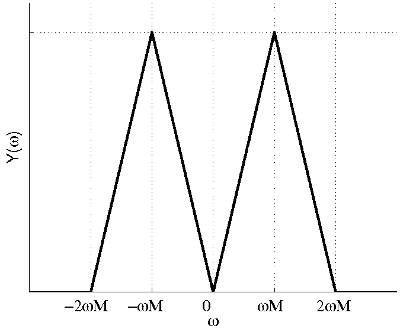
Thus the spectrum of $ y(t) $ is:
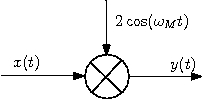
b) A block diagram of the scrambler that can generate the signal $ y(t) $ can be:
You can verify that by taking the FT of $ 2x(t)cos(\omega_M t) $.
c) The following block diagram describes a descrambler which can recover signal $ x(t) $ from $ y(t) $.
where $ \mathcal{H}(\omega)=\left\{\begin{array}{ll} 1, & \mbox{ for } |\omega|<\omega_M\\ 0, & \mbox{ elsewhere} \end{array}\right. $.
Note that $ \mathcal{H}(\omega) $ is the frequency response of a low pass filter with cut-off frequency equals to $ \omega_M $.
Question 4
a)
$ \begin{align} X(s)&=\int_{-\infty}^{\infty}e^{-5t}u(t+3)e^{-st} dt \\ &=\int_{-3}^{\infty}e^{-(5+s)t} dt \\ &=-\frac{1}{s+5}e^{-(5+s)t}|^{\infty}_{-3} \\ &=\frac{e^{3(5+s)}}{s+5} \end{align} $
where the ROC is:
- $ \mathcal{R}e\{5+s\}>0 $
- $ 5+\mathcal{R}e\{s\}>0 $
- $ \mathcal{R}e\{s\}>-5 $
b)
$ \begin{align} X(s)&=\int_{-\infty}^{\infty}e^{-5t}u(-t+5)e^{-st} dt \\ &=\int_{-\infty}^{5}e^{-(5+s)t} dt \\ &=-\frac{1}{s+5}e^{-(5+s)t}|_{-\infty}^{5} \\ &=-\frac{e^{-5(5+s)}}{s+5} \end{align} $
where the ROC is:
- $ \mathcal{R}e\{5+s\}<0 $
- $ 5+\mathcal{R}e\{s\}<0 $
- $ \mathcal{R}e\{s\}<-5 $
c)
$ \begin{align} X(s)&=\int_{-\infty}^{\infty}e^{-5t}[u(t)-u(t-3)]e^{-st} dt \\ &=\int_{0}^{3}e^{-(5+s)t} dt \\ &=-\frac{1}{s+5}[e^{-3(5+s)}-1]\\ &=\frac{1}{s+5}-\frac{e^{-3(5+s)}}{s+5} \end{align} $
where we did not need to constraint our result to a ROC (which is expected since the signal has finite duration).
d)
$ \begin{align} X(s)&=\int_{-\infty}^{\infty}e^{-2|t|}e^{-st}dt \\ &=\int_{-\infty}^{0}e^{2t}e^{-st}dt + \int_{0}^{\infty}e^-{2t}e^{-st}dt \\ &=\int_{-\infty}^{0}e^{(2-s)t}dt + \int_{0}^{\infty}e^-{(2+s)t}dt \\ &=\frac{1}{2-s}e^{(2-s)t}|^{0}_{-\infty}-\frac{1}{2+s}e^{-(2+s)t}|_{0}^{\infty} \\ &=\frac{1}{2-s}+\frac{1}{2+s} \end{align} $
where for the first term to converge we need $ \mathcal{R}e\{2-s\}>0 $, which is equivilant to $ \mathcal{R}e\{s\}<2 $, and for the other term to converge we need $ \mathcal{R}e\{2+s\}>0 $, or equivalently $ \mathcal{R}e\{s\}>-2 $.
Thus the ROC is the intersection of those two constraints and hence ROC is $ -2<\mathcal{R}e\{s\}<2 $.
Question 5
Since the Laplace transform of $ x(t) $ has exactly two poles at $ s=-1 $ and $ s=-3 $, then the ROC could be any of the following three:
- $ \mathcal{R}e\{s\}<-1 $
- $ \mathcal{R}e\{s\}<-3 $
- $ -3<\mathcal{R}e\{s\}<-1 $
But it is given that the FT of $ e^{2t}x(t) $ converges and hence $ s=-2 $ belongs to the ROC of the Laplace transform of $ x(t) $.
Hence the ROC is $ -3<\mathcal{R}e\{s\}<-1 $.
Since the ROC is $ -3<\mathcal{R}e\{s\}<-1 $, we deduce that the given signal is a sum of a right-sided signal and a left-sided signal. Thus, $ x(t) $ should be a two-sided signal.
Hence:
a) No
b) No
c) Yes
Question 6
In order to find the inverse Laplace transform of $ X(s) $, we need to find its partial fraction expansion.
First we compute the roots of the denominator, and then we get:
- $ X(s)=\frac{2(s+2)}{s^2+7s+12}=\frac{2(s+2)}{(s+3)(s+4)} $
Now we write:
- $ X(s)=\frac{A}{s+3}+\frac{B}{s+4} $
Multiplying both sides by $ (s+3)(s+4) $ and simplifying, we get:
- $ 2s+4=(A+B)s+4A+3B $
Comparing and solving, we have that: $ A=-2 $ and $ B=4 $.
Thus,
- $ X(s)=-\frac{2}{s+3}+\frac{4}{s+4} $
Now since the ROC is $ \mathcal{R}e\{s\}>-3 $, then $ x(t) $ should be a right sided signal or equivalently the sum of right sided signals. Hence,
- $ x(t)=[-2e^{-3t}+4e^{-4t}]u(t) $