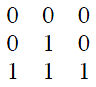m |
|||
| Line 26: | Line 26: | ||
* [[ECE438_Week14_Quiz_Q2sol|Solution]]. | * [[ECE438_Week14_Quiz_Q2sol|Solution]]. | ||
---- | ---- | ||
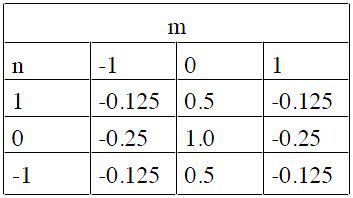
| + | Q3. Consider a 3 * 3 FIR filter with coefficients h[m, n] | ||
| + | |||
| + | [[Image:Q3_table.jpg]] | ||
| + | |||
| + | a. Find a difference equation that can be used to implement this filter. | ||
| + | |||
| + | b. Given an input image, find the center pixel value of output image. | ||
| + | |||
| + | [[Image:Q3_inputimg.jpg]] | ||
| + | |||
| + | c. Find a simple expression for the frequency response (DSFT) H(u,v) of this filter. | ||
| + | |||
| + | d. Plot H(u,v) along the u axis (v = 0) , along the v axis (u = 0) , along the line u = v , and along the line u = -v. | ||
| + | |||
| + | * [[ECE438_Week14_Quiz_Q3sol|Solution]]. | ||
| + | ---- | ||
| + | |||
Back to [[ECE438_Lab_Fall_2010|ECE 438 Fall 2010 Lab Wiki Page]] | Back to [[ECE438_Lab_Fall_2010|ECE 438 Fall 2010 Lab Wiki Page]] | ||
Back to [[2010_Fall_ECE_438_Boutin|ECE 438 Fall 2010]] | Back to [[2010_Fall_ECE_438_Boutin|ECE 438 Fall 2010]] | ||
Revision as of 09:50, 29 November 2010
Quiz Questions Pool for Week 14
Q1. Assume we know (or can measure) a function
$ \begin{align} p(x) &= \int_{-\infty}^{\infty}f(x,y)dy \end{align} $
Using the definition of the CSFT, derive an expression for F(u,0) in terms of the function p(x).
Q2. Consider the following 2D system with input x(m,n) and output y(m,n)
$ y(m,n) = x(m,n) + \lambda \left( x(m,n) - \frac{1}{9} \sum_{k=-1}^{1}\sum_{l=-1}^{1}x(m-k,n-l) \right) $
a. Is this a linear system? Is it space invariant?
b. What is the 2D impulse response of this system?
c. Calculate its frequency response H(u,v).
d. Describe how the filter behaves when $ \lambda $ is positive and large.
e. Describe how the filter behaves when $ \lambda $ is negative and bigger than -1.
Q3. Consider a 3 * 3 FIR filter with coefficients h[m, n]
a. Find a difference equation that can be used to implement this filter.
b. Given an input image, find the center pixel value of output image.
c. Find a simple expression for the frequency response (DSFT) H(u,v) of this filter.
d. Plot H(u,v) along the u axis (v = 0) , along the v axis (u = 0) , along the line u = v , and along the line u = -v.
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010