| Line 400: | Line 400: | ||
All 3 approaches lead to the same y[n]. | All 3 approaches lead to the same y[n]. | ||
---- | ---- | ||
| + | |||
| + | Q4. | ||
| + | <math> | ||
| + | H(z)= \frac{1-\frac{1}{2}z^{-2}} | ||
| + | {1-\frac{1}{\sqrt{2}} z^{-1} +\frac{1}{4} z^{-2}} | ||
| + | </math> | ||
| + | |||
| + | :a. Sketch the locations of the poles and zeros. | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | H(z) &= \frac{1-\frac{1}{2}z^{-2}}{1-\frac{1}{\sqrt{2}} z^{-1} +\frac{1}{4} z^{-2}} \\ | ||
| + | H(z) &= \frac{(z+\frac{1}{\sqrt{2}})(z-\frac{1}{\sqrt{2}})} | ||
| + | { (z-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(z-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | Zeros: <br/> | ||
| + | <math>z_1 = \frac{1}{\sqrt{2}}, z_2 = -\frac{1}{\sqrt{2}}</math><br/> | ||
| + | Poles: <br/> | ||
| + | <math>p_1 = \frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}, p_2 = \frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}}</math> | ||
| + | |||
| + | [[Image:Zp1.jpg]] | ||
| + | |||
| + | :b. Determine the magnitude and phase of the frequency response <math>H(\omega)</math>, for | ||
| + | |||
| + | ::<math>\omega =0,\frac{\pi}{4}, \frac{\pi}{2}, \frac{3\pi}{4}, \text{ and }\pi</math>. | ||
| + | |||
| + | :c. Is the system stable? Explain why or why not? | ||
| + | :d. Find the difference equation for y[n] in terms of x[n], corresponding to this transfer function H(z). | ||
| + | |||
Revision as of 11:56, 2 November 2010
Solution to HW7
Q1.
Recall, the Discrete Fourier Transform is defined as follows -
Definition: let x[n] be a DT signal with Period N. Then,
$ X [k] = \sum_{k=0}^{N-1} x[n].e^{-j2\pi kn/N} $
$ x [n] = (1/N) \sum_{k=0}^{N-1} X[k].e^{j2\pi kn/N} $
What is the relation between the DFT and the Fourier series coefficients of continuous periodic function x[n]?
The DFT of a sampled signal x[n] of length N is directly proportional to the Fourier series coefficients of the continuous periodic version of x[n].
The DFT of the N samples comprising one period of x[n] equals N times the Fourier series coefficients.
Alternatively -
The fourier series coefficients of a periodic, bandlimited signal x are given by the DFT of one period of the samples of x, divided by N, where N is the DFT length and N is also the number of samples in each period of x.
Credit: Julius Smith III, stanford.edu
$ x_1[n]= e^{j \frac{2}{3} \pi n}; $
Function's period N = 3,
Using IDFT,
$ \begin{align} x_1[n] &= \frac{1}{3} \sum_{k=0}^{2} X[k].e^{j2\pi kn/3} \\ e^{j \frac{2}{3} \pi n} &= \frac{1}{3} \sum_{k=0}^{2} X[k].e^{j2\pi kn/3} \\ &= \frac{1}{3} \left[ X[0].e^{j0} + X[1].e^{j2\pi n/3} + X[2].e^{j2\pi n(2/3)} \right] \\ &= \frac{1}{3} \left[ X[0] + X[1].e^{j2\pi n/3} + X[2].e^{j4\pi n/3} \right] \end{align} $
For the two sides to be equal,
X[0] = 0
X[1] = 3
X[2] = 0
Plugging in we can verify,
$ \begin{align} e^{j \frac{2}{3} \pi n} &= \frac{1}{3} \left[ 0 + 3.e^{j2\pi n/3} + 0 \right]\\ e^{j \frac{2}{3} \pi n} &= \frac{1}{3} 3.e^{j2\pi n/3} \\ e^{j \frac{2}{3} \pi n} &= e^{j \frac{2}{3} \pi n} \end{align} $
So our three selected values for X[k] are correct. Thus
$ X[k] = \begin{cases} 3, & k = 1 \\ 0, & \mbox{else} \end{cases} $
$ x_2[n]= e^{j \frac{2}{\sqrt{3}} \pi n}; $
Function x2[n] is aperiodic. Let's see why -
Assume x2[n] is periodic, then
$ e^{j \frac{2}{\sqrt{3}} \pi n} = e^{j \frac{2}{\sqrt{3}} \pi (n + N)} $ for function to be periodic, where N is an integer
$ e^{j \frac{2}{\sqrt{3}} \pi n} = e^{j \frac{2}{\sqrt{3}} \pi n}e^{j \frac{2}{\sqrt{3}} \pi N} $
$ e^{j \frac{2}{\sqrt{3}} \pi n} = e^{j \frac{2}{\sqrt{3}} \pi n}.(1) $
$ e^{j \frac{2}{\sqrt{3}} \pi N} = 1 $
For this to be true -
$ j \frac{2}{\sqrt{3}} \pi N = j 2\pi n, $ where n is an integer
$ N = n\sqrt{3} $
N is not an integer and this contradicts our assumption, proving that it cannot be true.
Thus, x_2[n] is aperiodic and we cannot apply the DFT.
$ x_3[n]= e^{j \frac{4}{3} \pi n}; $
Function's period N = 3,
Using IDFT,
$ \begin{align} x_3[n] &= \frac{1}{3} \sum_{k=0}^{2} X[k].e^{j2\pi kn/3} \\ e^{j \frac{4}{3} \pi n} &= \frac{1}{3} \sum_{k=0}^{2} X[k].e^{j2\pi kn/3} \\ &= \frac{1}{3} \left[ X[0].e^{j0} + X[1].e^{j2\pi n/3} + X[2].e^{j2\pi n(2/3)} \right] \\ &= \frac{1}{3} \left[ X[0] + X[1].e^{j2\pi n/3} + X[2].e^{j4\pi n/3} \right] \end{align} $
For the two sides to be equal,
X[0] = 0
X[1] = 0
X[2] = 3
$ X[k] = \begin{cases} 3, & k = 2 \\ 0, & \mbox{else} \end{cases} $
$ x_4[n]= e^{j \frac{2}{1000} \pi n}; $
Function's period N = 1000,
Using IDFT,
$ \begin{align} x_4[n] &= \frac{1}{1000} \sum_{k=0}^{999} X[k].e^{j2\pi kn/1000} \\ e^{j \frac{2}{1000} \pi n} &= \frac{1}{1000} \sum_{k=0}^{999} X[k].e^{j2\pi kn/1000} \\ &= \frac{1}{1000} \left[ X[0].e^{j0} + X[1].e^{j2\pi n/1000} + X[2].e^{j2\pi n(2/1000)} + ... \right] \\ &= \frac{1}{1000} \left[ X[0] + X[1].e^{j2\pi n/1000} + X[2].e^{j4\pi n/1000} + ... \right] \end{align} $
For the two sides to be equal,
X[0] = 0
X[1] = 1000
X[2] = 0
$ X[k] = \begin{cases} 1000, & k = 1 \\ 0, & \mbox{else} \end{cases} $
$ x_5[n]= e^{-j \frac{2}{1000} \pi n}; $
Function's period N = 1000,
$ \begin{align} x_5[n]&= e^{-j \frac{2}{1000} \pi n}.1 \\ &= e^{-j \frac{2}{1000} \pi n}.e^{-j 2\pi n} \\ &= e^{j 2\pi n(1 - (1/1000))} \\ &= e^{j 2\pi n\frac{999}{1000} } \\ \end{align} $
Using IDFT,
$ \begin{align} x_5[n] &= \frac{1}{1000} \sum_{k=0}^{999} X[k].e^{j2\pi kn/1000} \\ e^{j 2\pi n\frac{999}{1000}} &= \frac{1}{1000} \sum_{k=0}^{999} X[k].e^{j2\pi kn/1000} \\ &= \frac{1}{1000} \left[ X[0].e^{j0} + X[1].e^{j2\pi n/1000} + X[2].e^{j2\pi n(2/1000)}+ ... + X[999].e^{j2\pi n(999/1000)} \right] \\ &= \frac{1}{1000} \left[ X[0] + X[1].e^{j2\pi n/1000} + X[2].e^{j2\pi n (2/1000)} + ... + X[999].e^{j2\pi n(999/1000)} \right] \\ \end{align} $
For the two sides to be equal,
X[0] = 0
X[1] = 0
X[2] = 0
X[999] = 1000
$ X[k] = \begin{cases} 1000, & k = 999 \\ 0, & \mbox{else} \end{cases} $
$ \begin{align} x_6[n] &= \cos\left( \frac{2}{1000} \pi n\right) \\ &= \frac{1}{2}\left( e^{j\frac{2\pi n}{1000}} + e^{-j\frac{2\pi n}{1000}} \right) \\ &= \frac{1}{2} (x_4[n] + x_5[n]) \\ \end{align} $
We have an additional (1/2) to factor into the final coefficients, giving us -
$ X[k] = \begin{cases} 500, & k = 1 \\ 500, & k = 999 \\ 0, & \mbox{else} \end{cases} $
$ \begin{align} x_7[n] &= \cos^2\left( \frac{2}{1000} \pi n\right) \\ &= \left[ \frac{1}{2}\left( e^{j\frac{2\pi n}{1000}} + e^{-j\frac{2\pi n}{1000}} \right)\right]^2 \\ &= \frac{1}{4}\left( e^{j\frac{4\pi n}{1000}} + 2 + e^{-j\frac{4\pi n}{1000}} \right) \\ &= \frac{1}{4}\left( 2 + e^{j2\pi n\frac{2}{1000}} + e^{-j2\pi n\frac{2}{1000}}e^{-j2\pi n} \right) \\ &= \frac{1}{4}\left( 2 + e^{j2\pi n\frac{2}{1000}} + e^{j2\pi n\frac{998}{1000}} \right) \\ \end{align} $
Function's period N = 1000,
Using IDFT,
$ \begin{align} x_7[n] &= \frac{1}{1000} \sum_{k=0}^{999} X[k].e^{j2\pi kn/1000} \\ &= \frac{1}{1000} \left[ X[0] + X[1].e^{j2\pi n/1000} + X[2].e^{j2\pi n(2/1000)} + ... X[998].e^{j2\pi n(998/1000)} + X[999].e^{j2\pi n(999/1000)} \right] \\ \end{align} $
Comparing LHS and RHS,
X[0] = 2000
X[1] = 0
X[2] = 250
...
X[998] = 250
X[999] = 0
$ X[k] = \begin{cases} 2000, & k = 0 \\ 250, & k = 2 \\ 250, & k = 998 \\ 0, & \mbox{else} \end{cases} $
$ \begin{align} x_8[n]= (-j)^n \\ &= (e^{j \pi /2})^n \\ &= e^{j \pi n/2} \\ \end{align} $
Function's period N = 4,
Using IDFT,
$ \begin{align} x_8[n] &= \frac{1}{4} \sum_{k=0}^{3} X[k].e^{j2\pi kn/4} \\ e^{j \pi n/2} &= \frac{1}{4} \sum_{k=0}^{3} X[k].e^{j2\pi kn/4} \\ &= \frac{1}{4} \left[ X[0].e^{j0} + X[1].e^{j2\pi n/4} + X[2].e^{j2\pi n(2/4)} + X[3].e^{j2\pi n(3/4)}\right] \\ &= \frac{1}{4} \left[ X[0] + X[1].e^{j\pi n/2} + X[2].e^{j\pi n} + X[3].e^{j\pi n(3/2)} \right] \end{align} $
For the two sides to be equal,
X[0] = 0
X[1] = 4
X[2] = 0
X[2] = 0
$ X[k] = \begin{cases} 4, & k = 1 \\ 0, & \mbox{else} \end{cases} $
Q2.
$ y_1[n]= \frac{x[n]+x[n-1]}{2} $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y_1[z]&= \frac{X[z]+X[z].z^{-1}}{2} \\ \frac{Y_1[z]}{X[z]}&= \frac{1+z^{-1}}{2} \\ H_1[z] &= \frac{1+z^{-1}}{2} \\ \end{align} $
Frequency Response H_1($ \omega $),
$ \begin{align} H_1[e^{j\omega }] &= \frac{1+e^{-j\omega }}{2} \\ &= e^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}+e^{-j\frac{\omega }{2}}}{2} \right) \\ &= e^{-j\frac{\omega }{2}} cos \left( \frac{\omega }{2} \right) \\ \end{align} $
$ y_2[n]= \frac{x[n]-x[n-1]}{2} $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y_2[z]&= \frac{X[z]-X[z].z^{-1}}{2} \\ \frac{Y_2[z]}{X[z]}&= \frac{1-z^{-1}}{2} \\ H_2[z] &= \frac{1-z^{-1}}{2} \\ \end{align} $
Frequency Response H_2($ \omega $),
$ \begin{align} H_2[e^{j\omega }] &= \frac{1-e^{-j\omega }}{2} \\ &= e^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}-e^{-j\frac{\omega }{2}}}{2} \right) \\ &= je^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}-e^{-j\frac{\omega }{2}}}{2j} \right) \\ &= je^{-j\frac{\omega }{2}} sin \left( \frac{\omega }{2} \right) \\ \end{align} $
$ y_3[n]= \frac{x[n+1]+x[n]+x[n-1]}{3} $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y_3[z]&= \frac{X[z].z+ X[z] + X[z].z^{-1}}{3} \\ \frac{Y_3[z]}{X[z]}&= \frac{z(1+z^{-1} + z^{-2})}{3} \\ H_3[z] &= \frac{1+z^{-1} + z^{-2}}{3z^{-1}} \\ \end{align} $
Frequency Response H_3($ \omega $),
$ \begin{align} H_3[e^{j\omega }] &= \frac{1+e^{-j\omega }+e^{-j2\omega }}{3e^{-j\omega }} \\ &= \frac{e^{-j\omega }+e^{-j\omega }(e^{j\omega } + e^{-j\omega })}{3e^{-j\omega }} \\ &= \frac{e^{-j\omega }(1+2cos(\omega ))}{3e^{-j\omega }} \\ &= \frac{1+2cos(\omega )}{3} \\ \end{align} $
$ y_4[n]= \frac{x[n+1]-2 x[n]+x[n-1]}{4}. $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y_4[z]&= \frac{X[z].z- 2X[z] + X[z].z^{-1}}{4} \\ \frac{Y_3[z]}{X[z]}&= \frac{z(1-2z^{-1} + z^{-2})}{4} \\ H_3[z] &= \frac{1-2z^{-1} + z^{-2}}{4z^{-1}} \\ \end{align} $
Frequency Response H_3($ \omega $),
$ \begin{align} H_4[e^{j\omega }] &= \frac{1-2e^{-j\omega }+e^{-j2\omega }}{4e^{-j\omega }} \\ &= \frac{-2e^{-j\omega }+ 2 e^{-j\omega }\frac{(e^{j\omega } + e^{-j\omega })}{2}}{4e^{-j\omega }} \\ &= \frac{2e^{-j\omega }(cos(\omega )-1)}{4e^{-j\omega }} \\ &= \frac{cos(\omega )-1}{2} \\ \end{align} $
Q3.
a. Substituting values directly would yield the following -
$ \begin{align} n &= ...\text{ -3, -2, -1, 0, 1, 2, 3, 4, 5} ...\\ y\left[n\right] &= ...\text{ 0, -2, -4, -1, 2, -1, -4, -2, 0} ...\\ \end{align} $
b. h[n] = ?
Substitute x[n] = $ \delta[n] $ to obtain y[n] = h[n],
h[n] = $ \delta[n] $ + 2$ \delta[n-1] $ + $ \delta[n-2] $
Now x[n] = -2$ \delta[n+2] $ + $ \delta[n] $ - 2$ \delta[n-2] $
$ \begin{align} y[n] &= x[n] * h[n] \\ &= (-2\delta[n+2] + \delta[n] - 2\delta[n-2]) * (\delta[n] + 2\delta[n-1] + \delta[n-2]) \\ &= -2\delta[n+2] - 4\delta[n+1] -2\delta[n] + \delta[n] + 2\delta[n-1] + \delta[n-2] - 2\delta[n-2] - 4\delta[n-3] - 2\delta[n-4] \\ &= -2\delta[n+2] - 4\delta[n+1] - \delta[n] + 2\delta[n-1] - \delta[n-2] - 4\delta[n-3] = 2\delta[n-4] \\ \end{align} $
c. x[n] = $ e^{j\omega n} $
(i)
$ \begin{align} y[n] &= e^{j\omega n} + 2 e^{j\omega (n-1)} + e^{j\omega (n-2)} \\ &= e^{j\omega n}(1 + 2 e^{-j\omega } + e^{-2j\omega }) \\ H(e^{j\omega}) &= 1 + 2 e^{-j\omega } + e^{-2j\omega } \\ \end{align} $
(ii)
h[n] = $ \delta[n] $ + 2$ \delta[n-1] $ + $ \delta[n-2] $
H($ e^{j\omega} $) = 1 + 2 $ e^{-j\omega } $ + $ e^{-2j\omega } $
(i) and (ii) are the same.
d. x[n] = -2$ \delta[n+2] $ + $ \delta[n] $ - 2$ \delta[n-2] $
X($ e^{j\omega} $) = -2 $ e^{2j\omega } $ + 1 - 2$ e^{-2j\omega } $
$ \begin{align} Y(e^{j\omega}) &= X(e^{j\omega})H(e^{j\omega}) \\ &= (-2e^{2j\omega } + 1 - 2e^{-2j\omega } ).(1 + 2e^{-j\omega } + e^{-2j\omega }) \\ &= -2e^{2j\omega } - 4e^{j\omega } - 2 + 1 + 2e^{-j\omega } + 2e^{-2j\omega } - 2e^{-2j\omega } - 4e^{-3j\omega } - 2e^{-4j\omega } \\ &= -2e^{2j\omega } - 4e^{j\omega } - 1 - 2e^{-j\omega } - e^{-2j\omega } - 4e^{-3j\omega } - 2e^{-4j\omega } \\ \\ \text{Using Inverse DTFT,} \\ y[n] &= -2\delta[n+2] - 4\delta[n+1] - \delta[n] + 2\delta[n-1] - \delta[n-2] - 4\delta[n-3] - 2\delta[n-4] \\ \end{align} $
All 3 approaches lead to the same y[n].
Q4. $ H(z)= \frac{1-\frac{1}{2}z^{-2}} {1-\frac{1}{\sqrt{2}} z^{-1} +\frac{1}{4} z^{-2}} $
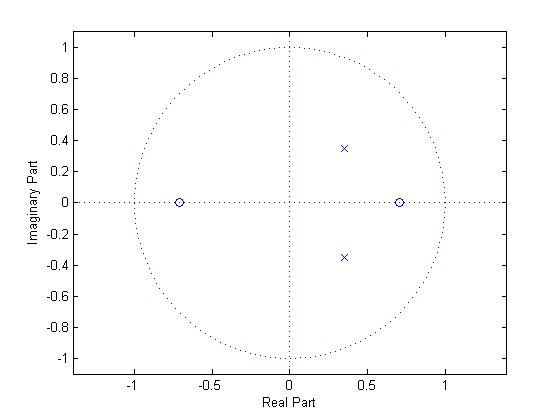
- a. Sketch the locations of the poles and zeros.
$ \begin{align} H(z) &= \frac{1-\frac{1}{2}z^{-2}}{1-\frac{1}{\sqrt{2}} z^{-1} +\frac{1}{4} z^{-2}} \\ H(z) &= \frac{(z+\frac{1}{\sqrt{2}})(z-\frac{1}{\sqrt{2}})} { (z-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(z-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \\ \end{align} $
Zeros:
$ z_1 = \frac{1}{\sqrt{2}}, z_2 = -\frac{1}{\sqrt{2}} $
Poles:
$ p_1 = \frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}, p_2 = \frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}} $
- b. Determine the magnitude and phase of the frequency response $ H(\omega) $, for
- $ \omega =0,\frac{\pi}{4}, \frac{\pi}{2}, \frac{3\pi}{4}, \text{ and }\pi $.
- c. Is the system stable? Explain why or why not?
- d. Find the difference equation for y[n] in terms of x[n], corresponding to this transfer function H(z).
Back to HW7
Back to ECE 438 Fall 2010