| Line 77: | Line 77: | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| − | X_N(k)&=\sum_{n=0}^{ | + | X_N(k)&=\sum_{n=0}^{N-1} x(n)e^{-\frac{j2\pi kn}{N}} \\ |
&\text{Change variable n=2m+l, m=0,1,2; l=0,1 } \\ | &\text{Change variable n=2m+l, m=0,1,2; l=0,1 } \\ | ||
| − | X_N(k)&=\sum_{l=0}^{1}\sum_{m=0}^{2}x(2m+l)e^{-\frac{j2\pi k(2m+l)}{ | + | X_N(k)&=\sum_{l=0}^{1}\sum_{m=0}^{2}x(2m+l)e^{-\frac{j2\pi k(2m+l)}{N}} \\ |
| − | &=\sum_{l=0}^{1}e^{-\frac{j2\pi kl}{ | + | &=\sum_{l=0}^{1}e^{-\frac{j2\pi kl}{N}}\sum_{m=0}^{2}x(2m+l)e^{-\frac{j2\pi km)}{N/2}} \\ |
| − | &=\sum_{l=0}^{1}W_N^{kl}X_l(k) \text{k=0,1,..., | + | &=\sum_{l=0}^{1}W_N^{kl}X_l(k) \text{k=0,1,...,N-1 } |
\end{align} | \end{align} | ||
</math> | </math> | ||
| Line 103: | Line 103: | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| − | X_N(k)&=\sum_{n=0}^{ | + | X_N(k)&=\sum_{n=0}^{N-1} x(n)e^{-\frac{j2\pi kn}{N}} \\ |
&\text{Change variable n=3m+l, m=0,1; l=0,1,2 } \\ | &\text{Change variable n=3m+l, m=0,1; l=0,1,2 } \\ | ||
| − | X_N(k)&=\sum_{l=0}^{2}\sum_{m=0}^{1}x(3m+l)e^{-\frac{j2\pi k(3m+l)}{ | + | X_N(k)&=\sum_{l=0}^{2}\sum_{m=0}^{1}x(3m+l)e^{-\frac{j2\pi k(3m+l)}{N}} \\ |
| − | &=\sum_{l=0}^{2}e^{-\frac{j2\pi kl}{ | + | &=\sum_{l=0}^{2}e^{-\frac{j2\pi kl}{N}}\sum_{m=0}^{1}x(3m+l)e^{-\frac{j2\pi km)}{N/3}} \\ |
| − | &=\sum_{l=0}^{2}W_N^{kl}X_l(k) \text{k=0,1,..., | + | &=\sum_{l=0}^{2}W_N^{kl}X_l(k) \text{k=0,1,...,N-1 } |
\end{align} | \end{align} | ||
</math> | </math> | ||
| Line 124: | Line 124: | ||
Q4. | Q4. | ||
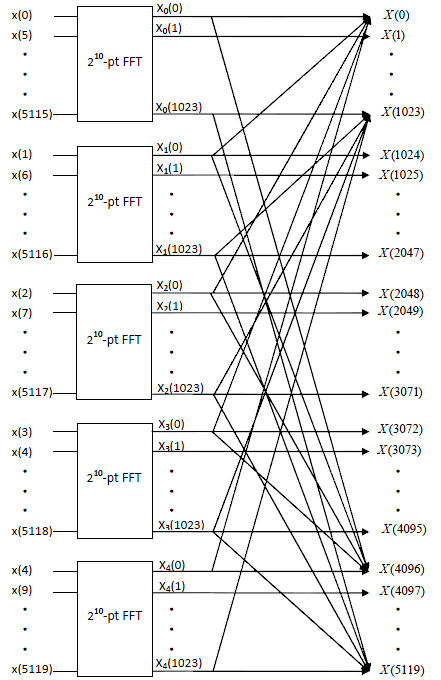
| + | Flow Diagram: | ||
| + | |||
| + | [[Image:HW6_Q4_FFT.jpg]] | ||
| + | |||
| + | <math>5120=5*1024=5*2^10</math> So we can split the 5120-point DFT into 5 1024-point DFTs using decimation-in-time and compute the 1024-point DFT using the subroutine of radix 2 FFT. | ||
| + | |||
| + | Analytical expression: | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | X^{(5120)}(k)&=\sum_{n=0}^{5119} x(n)e^{-\frac{j2\pi kn}{5120}} \\ | ||
| + | &\text{Change variable n=5m+l, m=0,1,...,1023; l=0,1,...,4 } \\ | ||
| + | X^{(5120)}(k)&=\sum_{l=0}^{4}\sum_{m=0}^{1023}x(5m+l)e^{-\frac{j2\pi k(5m+l)}{5120}} \\ | ||
| + | &=\sum_{l=0}^{4}e^{-\frac{j2\pi kl}{5120}}\sum_{m=0}^{1023}x(5m+l)e^{-\frac{j2\pi km)}{1024}} \\ | ||
| + | &=\sum_{l=0}^{4}W_{5120}^{kl}X_l^{(1024)}(k) \text{k=0,1,...,5119 } | ||
| + | \end{align} | ||
| + | </math> | ||
------------------------------------ | ------------------------------------ | ||
Revision as of 05:20, 20 October 2010
Homework 6 Solution
Q1.
Matlab code:
Assign the value of parameters and then call the function signalDFT
For example, in case 6 type following command in the command window of Matlab:
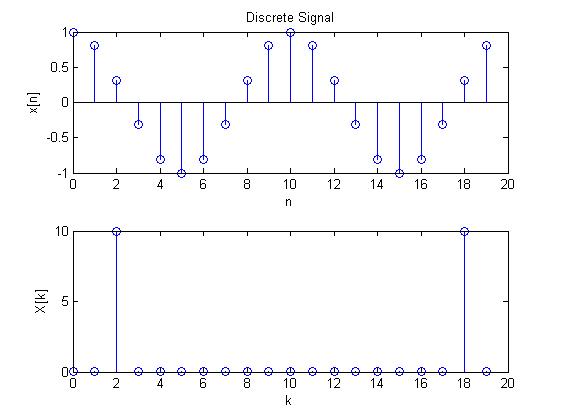
N=20;
w1=0.62831853;
k=0.2;
w2=0.79168135;
[x,X]=signal(w1,w2,k,N);
Plot result:
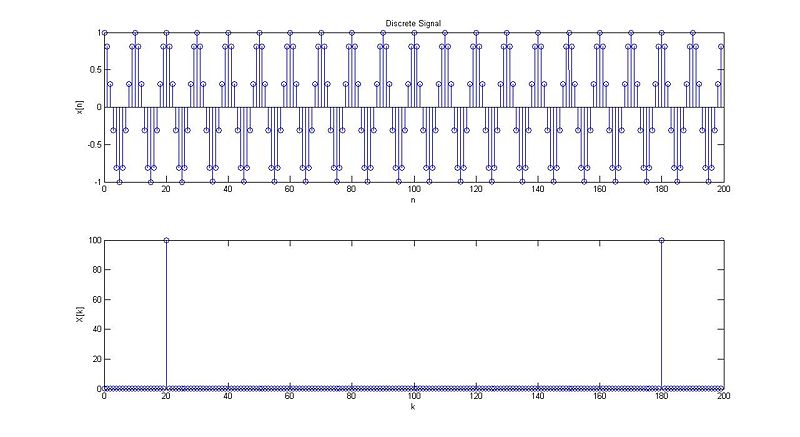
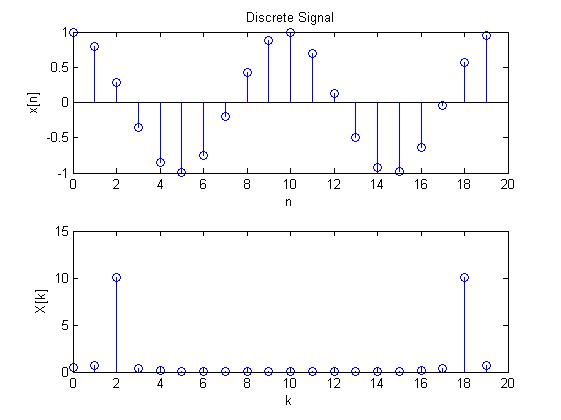
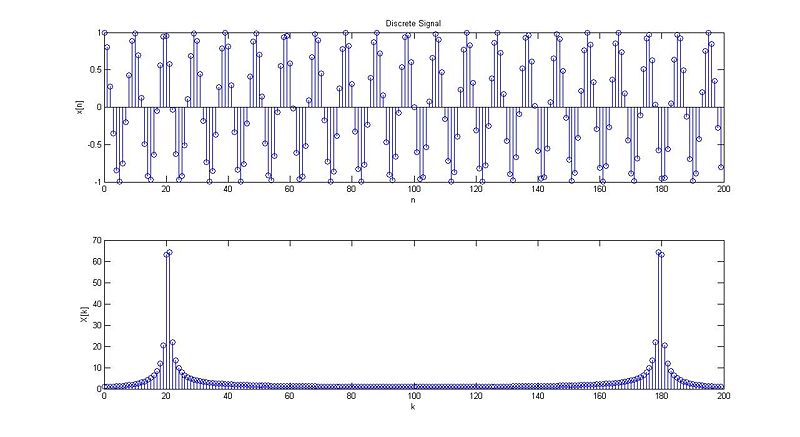
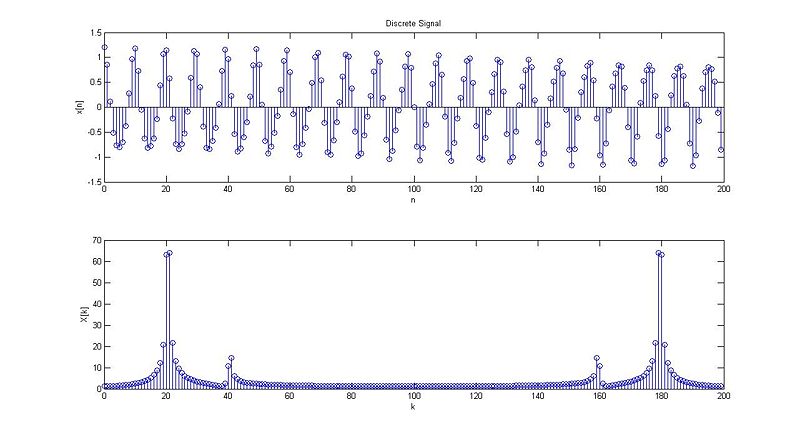
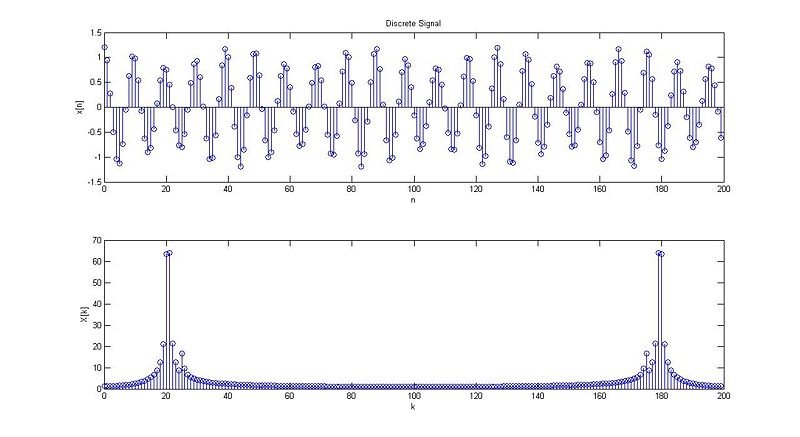
case 1:
case 2:
case 3:
case 4:
case 5:
case 6:
Q2.
Recall the definition of DFT: $ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N} $
In this question N=8
If we use summation formula to compute DFT, for each k, we need N times complex multiplications and N times complex additions.
In total, we need N*N=64 times of complex multiplications and N*(N-1)=56 times of complex additions.
In decimation-in-time FFT algorithm, we keep on decimating the number of points by 2 until we get 2 points DFT. At most, we can decimate $ v=log_2 N $ times. As a result, we get v levels of DFT. For each level, we need N/2 times of complex multiplications and N times of complex additions.
In total, we need $ \frac{N}{2}log_2 N=12 $N times of complex multiplications and $ Nlog_2 N=24 $ times of complex additions.
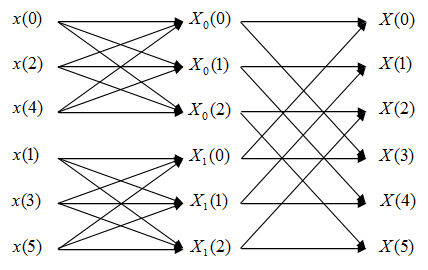
Q3.
Denote N is the points number of the input signal's DFT. Then N=6.
1) The normal DFT algorithm: If we use summation formula to compute DFT, according to the analysis of Q2. We need N*N=36 times of complex multiplications and N*(N-1)=30 times of complex additions.
Flow diagram of FFT:
Analytical Expressions:
$ \begin{align} X_N(k)&=\sum_{n=0}^{N-1} x(n)e^{-\frac{j2\pi kn}{N}} \\ &\text{Change variable n=2m+l, m=0,1,2; l=0,1 } \\ X_N(k)&=\sum_{l=0}^{1}\sum_{m=0}^{2}x(2m+l)e^{-\frac{j2\pi k(2m+l)}{N}} \\ &=\sum_{l=0}^{1}e^{-\frac{j2\pi kl}{N}}\sum_{m=0}^{2}x(2m+l)e^{-\frac{j2\pi km)}{N/2}} \\ &=\sum_{l=0}^{1}W_N^{kl}X_l(k) \text{k=0,1,...,N-1 } \end{align} $
In this FFT algorithm, the computing of DFT is divided into two levels. First, we compute two 3-point DFT, which are DFT of even and odd points.
In this step we need 4 times of complex multiplications and 6 times of complex additions for each 3-point DFT. Since we have to do this twice, we need 4*2=8 times of complex multiplications and 6*2=12 times of complex additions.
Second, we compute the final DFT by combing the first level result. According to the analysis of Q2, we need N/2=3 times of complex multiplications and N=6 times of complex additions.
In total, we need 8+3=11 times of complex multiplications and 12+6=18 times of complex additions.
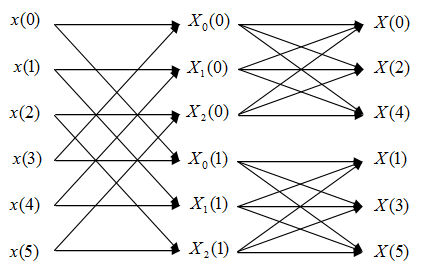
2)
Flow diagram of FFT:
Analytical Expressions:
$ \begin{align} X_N(k)&=\sum_{n=0}^{N-1} x(n)e^{-\frac{j2\pi kn}{N}} \\ &\text{Change variable n=3m+l, m=0,1; l=0,1,2 } \\ X_N(k)&=\sum_{l=0}^{2}\sum_{m=0}^{1}x(3m+l)e^{-\frac{j2\pi k(3m+l)}{N}} \\ &=\sum_{l=0}^{2}e^{-\frac{j2\pi kl}{N}}\sum_{m=0}^{1}x(3m+l)e^{-\frac{j2\pi km)}{N/3}} \\ &=\sum_{l=0}^{2}W_N^{kl}X_l(k) \text{k=0,1,...,N-1 } \end{align} $
In this FFT algorithm, the computing of DFT is still divided into two levels. However, we will first compute three 2 points DFT, which are DFT of the first half points and the second half points. According to analysis of Q2, we need N/2=3 times of complex multiplications and N=6 times of complex additions.
Second, we compute the two 3 points DFT using first level result. we need 4 times of complex multiplications and 6 times of complex additions for each 3-point DFT. Since we have to do this twice, we need 4*2=8 times of complex multiplications and 6*2=12 times of complex additions.
In total, we need 3+8=11 times of complex multiplications and 6+12=18 times of complex additions.
Notice that the output sequences of DFT of 2) is different from 1).
Compare 1) and 2), both methods have the same amount of complex operations.
Q4.
Flow Diagram:
$ 5120=5*1024=5*2^10 $ So we can split the 5120-point DFT into 5 1024-point DFTs using decimation-in-time and compute the 1024-point DFT using the subroutine of radix 2 FFT.
Analytical expression:
$ \begin{align} X^{(5120)}(k)&=\sum_{n=0}^{5119} x(n)e^{-\frac{j2\pi kn}{5120}} \\ &\text{Change variable n=5m+l, m=0,1,...,1023; l=0,1,...,4 } \\ X^{(5120)}(k)&=\sum_{l=0}^{4}\sum_{m=0}^{1023}x(5m+l)e^{-\frac{j2\pi k(5m+l)}{5120}} \\ &=\sum_{l=0}^{4}e^{-\frac{j2\pi kl}{5120}}\sum_{m=0}^{1023}x(5m+l)e^{-\frac{j2\pi km)}{1024}} \\ &=\sum_{l=0}^{4}W_{5120}^{kl}X_l^{(1024)}(k) \text{k=0,1,...,5119 } \end{align} $
Q5.
Q6.
Q7.