(New page: Category:2010 Fall ECE 438 Boutin ---- == Solution to Q1 of Week 8 Quiz Pool == ---- <math>\begin{align} \text{(a)} \quad & y[n] = 0.6 y[n-1] + 0.4 x[n] \\ & h[n] = 0.6h[n-1] + 0.4\d...) |
|||
| Line 13: | Line 13: | ||
<math>\begin{align} | <math>\begin{align} | ||
| − | {\color{White}abcde} & h[0]=0. | + | {\color{White}abcde} & h[0]=0.4 \\ |
| − | & h[1]=0. | + | & h[1]=0.6h[0]=0.4 \times 0.6 \\ |
| − | & h[2]=0. | + | & h[2]=0.6h[1]=0.4 \times (0.6)^2 \\ |
& \ldots \\ | & \ldots \\ | ||
| − | & h[n] = 0. | + | & h[n] = 0.4(0.6)^n u[n] \\ |
\end{align}</math> | \end{align}</math> | ||
| Line 44: | Line 44: | ||
---- | ---- | ||
| − | |||
Back to [[ECE438_Week8_Quiz|Lab Week 8 Quiz Pool]] | Back to [[ECE438_Week8_Quiz|Lab Week 8 Quiz Pool]] | ||
Latest revision as of 10:03, 13 October 2010
Solution to Q1 of Week 8 Quiz Pool
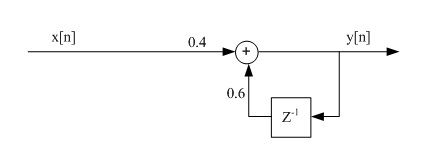
$ \begin{align} \text{(a)} \quad & y[n] = 0.6 y[n-1] + 0.4 x[n] \\ & h[n] = 0.6h[n-1] + 0.4\delta[n] \\ \end{align}\,\! $
assume that $ h[n]=0 $ when $ n<0 $.
$ \begin{align} {\color{White}abcde} & h[0]=0.4 \\ & h[1]=0.6h[0]=0.4 \times 0.6 \\ & h[2]=0.6h[1]=0.4 \times (0.6)^2 \\ & \ldots \\ & h[n] = 0.4(0.6)^n u[n] \\ \end{align} $
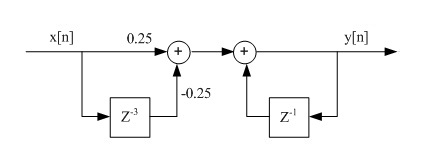
$ \begin{align} \text{(b)} \quad & y[n] = y[n-1] + 0.25 (x[n]-x[n-3]) \\ & h[n] = h[n-1] + 0.25(\delta[n]-\delta[n-3]) \\ \end{align}\,\! $
assume that $ h[n]=0 $ when $ n<0 $.
$ \begin{align} {\color{White}abcde} & h[0]=0.25 \\ & h[1]=h[0]=0.25 \\ & h[2]=h[1]=0.25 \\ & h[3]=h[2]-0.25=0 \\ & h[4]=h[3]=0 \\ & \ldots \\ & h[n] = 0.25(u[n]-u[n-3]) \\ \end{align} $
Back to Lab Week 8 Quiz Pool
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010