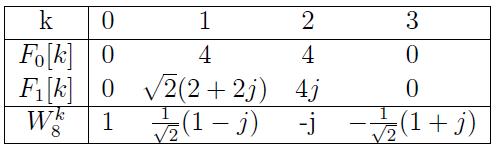| Line 31: | Line 31: | ||
Given the values of <math>X_8[k]</math> for k = 0, 1, ..., 7 determined in Q1, determine the numerical values of <math>k_1\text{ and }k_2</math>. | Given the values of <math>X_8[k]</math> for k = 0, 1, ..., 7 determined in Q1, determine the numerical values of <math>k_1\text{ and }k_2</math>. | ||
| − | |||
Answer [[W7Q2Sol|Here]]. | Answer [[W7Q2Sol|Here]]. | ||
Revision as of 16:15, 3 October 2010
Week7 Quiz Pool
Q1: As part of the first stage in a radix 2 FFT, a sequence x[n] of length N = 8 is decomposed into two sequences of length 4 as
$ f_0[n] = x[2n]\text{ , n = 0, 1, 2, 3} $
$ f_1[n] = x[2n + 1]\text{ , n = 0, 1, 2, 3} $
The 4-pt. DFT of each of these two sequences is $ F_0[k]\text{ and }F_1[k] $ respectively.
The specific values of $ F_0[k]\text{ and }F_1[k] $, k = 0, 1, 2, 3, obtained from the length N = 8 sequence in question are listed in the Table below.
From the values of $ F_0[k] \text{ and }F_1[k] $, k = 0, 1, 2, 3, and the values of
$ W_8^k = e^{\frac{-j2\pi k}{8}}, k = 0, 1, 2, 3 $
provided in the Table, determine the numerical values of the actual N = 8-pt. DFT of x[n] denoted $ X_8[k] $ for k = 0, 1, 2, 3, 4, 5, 6, 7.
Answer Here.
Q2: The underlying length N = 8 sequence of x[n] in Q1 may be expressed as
$ x[n] = e^{j2\pi k_1n/8} + e^{j2\pi k_2n/8}, n = 0,1,2 ..., 7 $
Given the values of $ X_8[k] $ for k = 0, 1, ..., 7 determined in Q1, determine the numerical values of $ k_1\text{ and }k_2 $.
Answer Here.
Q3:
Q4:
Q5:
Q6: