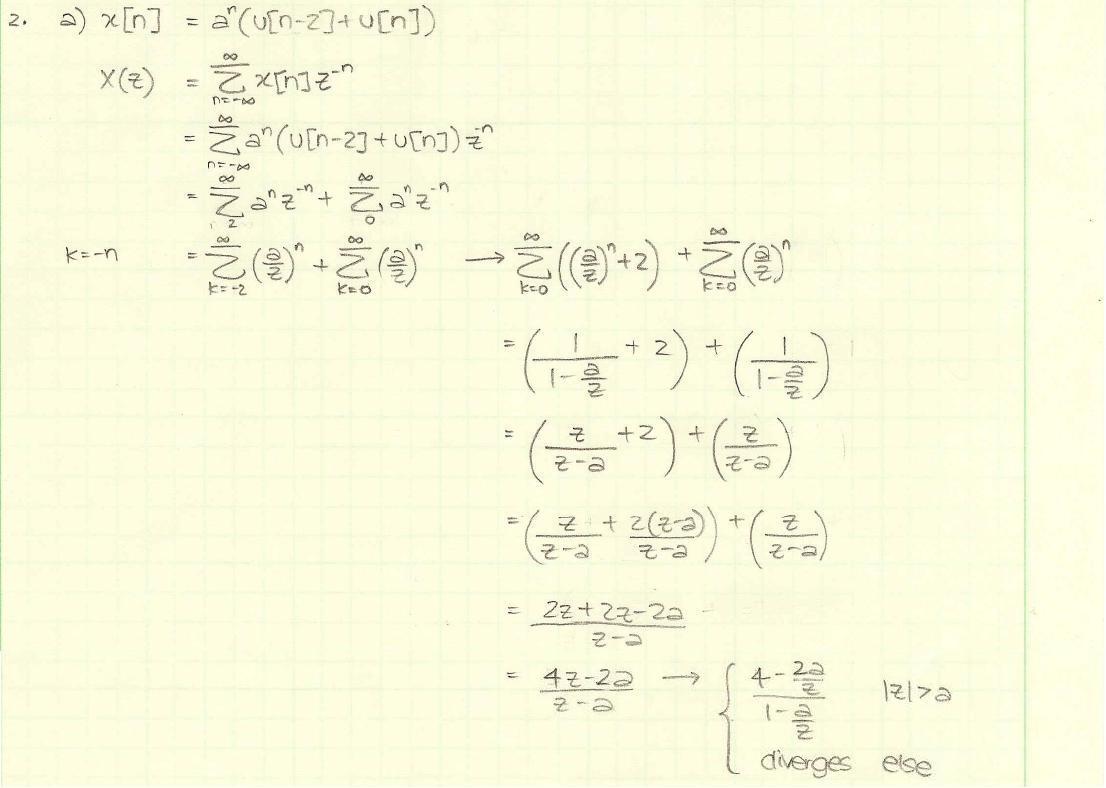m |
|||
| Line 1: | Line 1: | ||
I'm not sure if I've done this correctly in the first place. I would like your input before I actually attempt to inverse it. | I'm not sure if I've done this correctly in the first place. I would like your input before I actually attempt to inverse it. | ||
| − | Thank you. | + | Thank you. |
| + | **I will type this out properly at some point. | ||
[[Image:inverseatransformksoong.jpg]] | [[Image:inverseatransformksoong.jpg]] | ||
Revision as of 20:36, 11 September 2010
I'm not sure if I've done this correctly in the first place. I would like your input before I actually attempt to inverse it. Thank you.
- I will type this out properly at some point.
- EDIT: I have realized at least that my ROCs have been backwards. I had understood it as trying to make the 1/z term go to zero to converge. Well, that's wrong.
- ~ksoong
Answer from Prof. MImi
- In the step where you replaced -n by k, you forgot to replace the n inside the summation. Also, the first sum should then go from -2 to -infinity, instead of infinity.
- Actually, I do not see why you replaced -n by k in both sums. IN the first sum, you should have set k=n-2. In the second sum, you did not need to make any change of variable.
- The arrow in the middle of your computations, and the one towards the end should both be replaced by equal signs.
- The simplification of the first summation following the arrow is incorrect: you would need to add two terms instead of just one.
- The equality following the arrow is only valid when |z|>|a|.You must write this next to the equality!
- This explanation would be much clearer if you had typed in your answer: this way I could make notes directly inside the computations and cross-out and replace stuff using different colors.
Anybody sees anything else? Do you have more questions?