| Line 1: | Line 1: | ||
| − | ==A Solution Method For Zero-Dimensional Polynomial Equation System== | + | == A Solution Method For Zero-Dimensional Polynomial Equation System == |
| − | '''Motivation''' | + | '''Motivation''' |
| − | <div style= | + | <div style="width: 70%; float: left;"> |
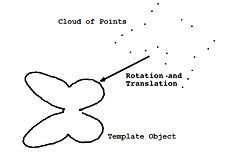
| − | Consider the problem of curve registration, that is, finding the rotation and translation that best maps (i.e., registers) a cloud of points onto a template object, as described on the right. | + | Consider the problem of curve registration, that is, finding the rotation and translation that best maps (i.e., registers) a cloud of points onto a template object, as described on the right. |
| − | We | + | We first approximate the curve defined by the contour of the template object by an implicit polynomial equation. This yields a bivariate polynomial equation p(x,y) = 0 whose solution set approximates the template contour. |
| − | polynomial equation p(x,y) = 0 whose solution set approximates the template | + | |
| − | contour. | + | Let (x_i,y_i) , i=1, ..., N be the points of the point cloud. We are looking for the rotation R and the translation T such that p((xi, yi)R + T) = 0 for all i = 1, ..., N. Then we have an overdetermined polynomial equation system with noisy coefficient, which contains N equations and unknown variables R and T. We need to solve this overdetermined polynomial system. |
| − | </div> | + | </div> <div style="width: 30%; float: right;"> |
| − | <div style= | + | [[Image:Butterfly model.jpg|250px]] |
| − | [[Image: | + | </div> <div style="width: 100%; float: left;"></div> |
| − | </div> | + | |
| − | <div style= | + | |
Revision as of 17:05, 21 April 2010
A Solution Method For Zero-Dimensional Polynomial Equation System
Motivation
Consider the problem of curve registration, that is, finding the rotation and translation that best maps (i.e., registers) a cloud of points onto a template object, as described on the right.
We first approximate the curve defined by the contour of the template object by an implicit polynomial equation. This yields a bivariate polynomial equation p(x,y) = 0 whose solution set approximates the template contour.
Let (x_i,y_i) , i=1, ..., N be the points of the point cloud. We are looking for the rotation R and the translation T such that p((xi, yi)R + T) = 0 for all i = 1, ..., N. Then we have an overdetermined polynomial equation system with noisy coefficient, which contains N equations and unknown variables R and T. We need to solve this overdetermined polynomial system.