| Line 55: | Line 55: | ||
[[User:Pritchey|Pritchey]] 20:28, 9 April 2010 (UTC) | [[User:Pritchey|Pritchey]] 20:28, 9 April 2010 (UTC) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
---- | ---- | ||
[[ 2010 Spring ECE 662 mboutin|Back to 2010 Spring ECE 662 mboutin]] | [[ 2010 Spring ECE 662 mboutin|Back to 2010 Spring ECE 662 mboutin]] | ||
Revision as of 05:17, 12 April 2010
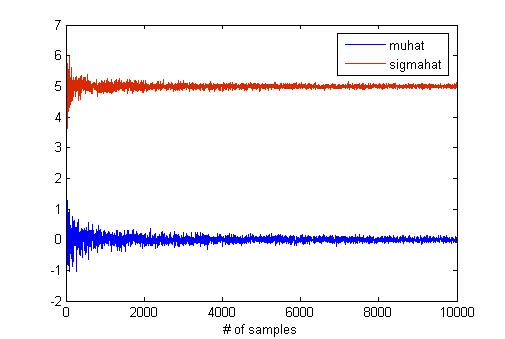
MATLAB has a "mle" function for maximum likelihood estimation. I think that this function is useful to verify the result of hw2 if you have MATLAB. I try to find the effect of the sample size in MLE using "mle" function because the number of samples is critical for estimation. To do this, I generate samples from normal distribution with mean as 0 and std as 5. The below graph shows the results of MLE according to the number of samples.
The code for this graph is like below.
samples_step = 3;
num_samples = samples_step:samples_step:10000;
len = length(num_samples);
mu = 0;
sigma = 5;
muhat = zeros(1, len);
sigmahat = zeros(1, len);
for x = num_samples
data = mu + sigma * randn(1, x);
phat = mle(data(1, :));
muhat(1, x/samples_step) = phat(1);
sigmahat(1, x/samples_step) = phat(2);
end
plot(num_samples, muhat);
hold on;
plot(num_samples, sigmahat);
--Han84 22:49, 2 April 2010 (UTC)
Need real database? Look it up in this website:
http://archive.ics.uci.edu/ml/datasets.html
have fun!
Golsa
Cholesky Decomposition
I wrote this MATLAB / FreeMat code to compute the Cholesky Decomposition of a matrix. The matrix A should be real and positive definite.
function L = cholesky(A)
N = length(A);
L = zeros(N);
for i=1:N
for j=1:i-1
L(i,j) = 1/L(j,j) * (A(i,j) - L(i,1:j-1)*L(j,1:j-1)');
end
L(i,i) = sqrt(A(i,i) - L(i,1:i-1)*L(i,1:i-1)');
end
end
You can use the resulting lower triangular matrix L to generate multivariate normal samples with covariance given by the matrix A by computing
X = $ \mu $ + L Z, where Z is iid standard normal.
Pritchey 20:28, 9 April 2010 (UTC)