| Line 17: | Line 17: | ||
For those familiar with the properties of the 1D Fourier Transform (FT), the 2-D Continuous-Space Fourier Transform (CSFT) is an intuitive extension of the 1D properties. The following rhea link shows some of these properties: [https://kiwi.ecn.purdue.edu/rhea/index.php/Student_summary_spectral_analysis_2D_signals] | For those familiar with the properties of the 1D Fourier Transform (FT), the 2-D Continuous-Space Fourier Transform (CSFT) is an intuitive extension of the 1D properties. The following rhea link shows some of these properties: [https://kiwi.ecn.purdue.edu/rhea/index.php/Student_summary_spectral_analysis_2D_signals] | ||
| − | Let's look at what the 2D FFT of Lena looks like. We will look at some simple 3X3 filters that are then convolved with the original image to create a filtered image. '' | + | Let's look at what the 2D FFT of Lena looks like. We will look at some simple 3X3 filters that are then convolved with the original image to create a filtered image. ''[Here is an excellent webpage showing how 2D convolution works: [http://www.songho.ca/dsp/convolution/convolution2d_example.html]]''<br><br> |
The following pictures show the original image (Lena), the image of the filter, and the filtered image (done with conv2). MATLAB m-files available upon request. | The following pictures show the original image (Lena), the image of the filter, and the filtered image (done with conv2). MATLAB m-files available upon request. | ||
| Line 25: | Line 25: | ||
Let's start with the filter = 1/16*[1 2 1; 2 4 2; 1 2 1], commonly referred to as an "average filter": | Let's start with the filter = 1/16*[1 2 1; 2 4 2; 1 2 1], commonly referred to as an "average filter": | ||
[[Image:Filter1_image.png|thumbnail|left|800px]] | [[Image:Filter1_image.png|thumbnail|left|800px]] | ||
| − | Can you tell that the filtered image is "smoothed"? Let's look at the images as 3-dimensional projections for easier visualization (via MATLAB's mesh command) | + | Can you tell that the filtered image is "smoothed"? Let's look at the images as 3-dimensional projections for easier visualization (via MATLAB's mesh command). First the original image: |
[[Image:MeshOriginal.png|thumbnail|left|400px]]Notice that the following filtered image has much more gradual color gradations (e.g. the red "lingers around longer" and there is less blue; this is because this filter acts as a low pass filter, removing high frequency components!): [[Image:MeshFiltered.png|thumbnail|left|400px]] | [[Image:MeshOriginal.png|thumbnail|left|400px]]Notice that the following filtered image has much more gradual color gradations (e.g. the red "lingers around longer" and there is less blue; this is because this filter acts as a low pass filter, removing high frequency components!): [[Image:MeshFiltered.png|thumbnail|left|400px]] | ||
Revision as of 17:37, 25 November 2009
Spectral Analysis of 2D Signals (December 1, 2009)
Here, I will describe and explain the basics behind analyzing the spectrum of 2-D signals - principally images! - Ryan Scheidt
The following image, commonly referred to as "Lena" (sometimes also "Lenna"), is a famous image utilized in standard image processing algorithms and testing. The background behind this image is quite interesting. Here are some links for the interested reader: [1], [2]
Spectral analysis of two-dimensional (2D) signals is not much different than the familiar one-dimensional (1D) FFT (Fast Fourier Transform - [3]) that we are (more) accustomed to. The only difference is that our signals are now represented in one more plane. We can think of this difference (1D vs. 2D) as the difference between, say, a one-dimensional longitudinal wave in a slinky (like this: [4]), versus a two-dimensional wave from a trampoline (e.g. drop a baseball in the center (or given any other excitation), and the wave will propagate in both x and y-directions ([5]).
For those familiar with the properties of the 1D Fourier Transform (FT), the 2-D Continuous-Space Fourier Transform (CSFT) is an intuitive extension of the 1D properties. The following rhea link shows some of these properties: [6]
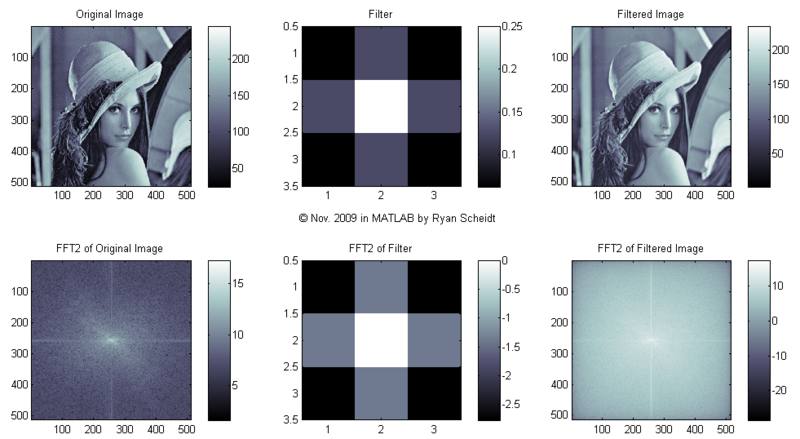
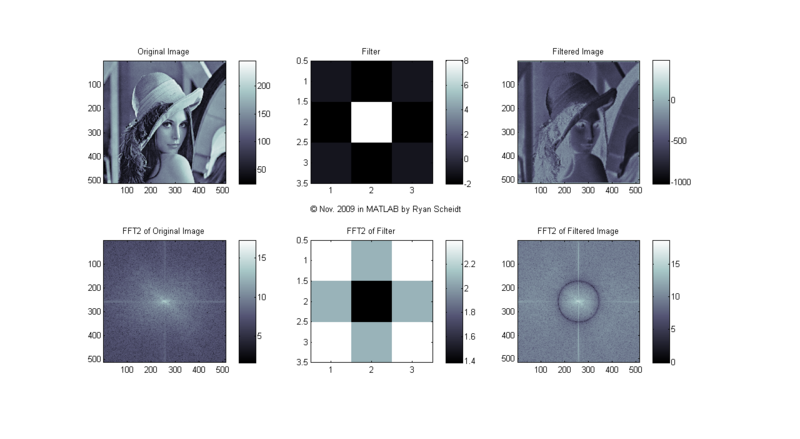
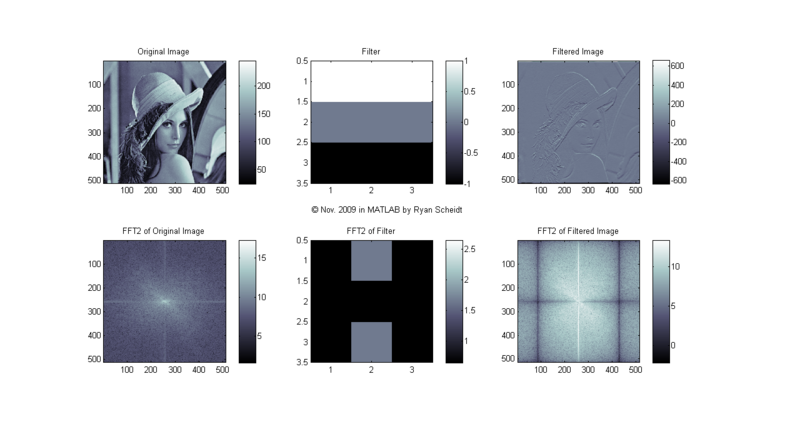
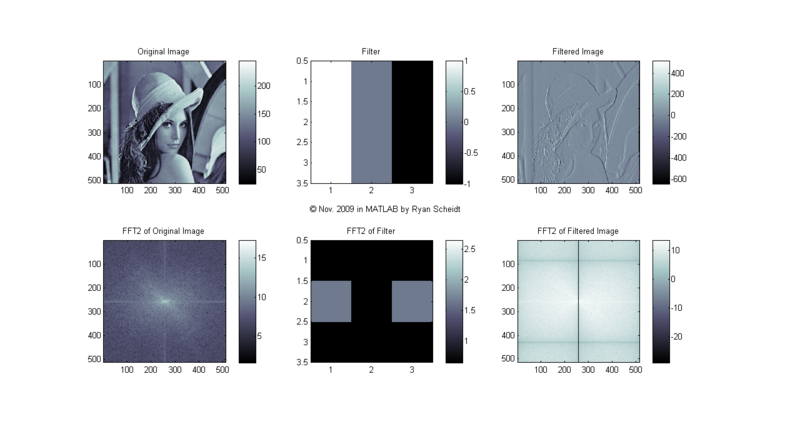
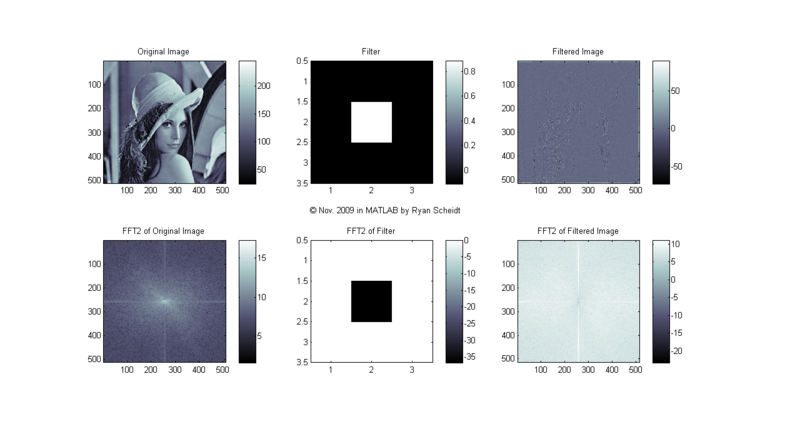
Let's look at what the 2D FFT of Lena looks like. We will look at some simple 3X3 filters that are then convolved with the original image to create a filtered image. [Here is an excellent webpage showing how 2D convolution works: [7]]
The following pictures show the original image (Lena), the image of the filter, and the filtered image (done with conv2). MATLAB m-files available upon request.
The colormaps to the right of each image show the corresponding values for each shade of gray (i.e. continuum from white to black). Each image is "normalized to 256 values" so that for each pixel, the lowest values (even if negative) are mapped to 0 (black) and the highest values are mapped to 255 (white).
(Note: click on the following images and follow "Full resolution" hyperlink to see full image.)
Let's start with the filter = 1/16*[1 2 1; 2 4 2; 1 2 1], commonly referred to as an "average filter":
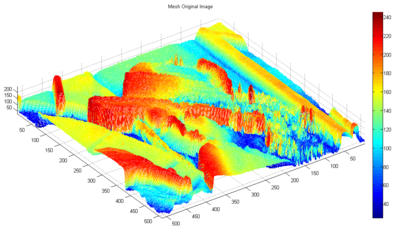
Can you tell that the filtered image is "smoothed"? Let's look at the images as 3-dimensional projections for easier visualization (via MATLAB's mesh command). First the original image:
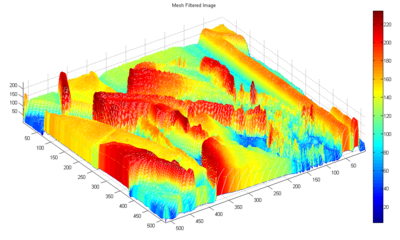
Notice that the following filtered image has much more gradual color gradations (e.g. the red "lingers around longer" and there is less blue; this is because this filter acts as a low pass filter, removing high frequency components!):