(→Three crucial questions to answer) |
(→Three crucial questions to answer) |
||
| Line 25: | Line 25: | ||
Impurity is large when the training data contain equal percentages of each class | Impurity is large when the training data contain equal percentages of each class | ||
| − | <math> P(\omega _i) = \frac{1}{C} </math>; for all <math>i</math> | + | <math>P(\omega _i) = \frac{1}{C}</math>; for all <math>i</math> |
Let <math> I </math> denote the impurity. Impurity can be defined in the following ways: | Let <math> I </math> denote the impurity. Impurity can be defined in the following ways: | ||
| Line 31: | Line 31: | ||
* "Entropy Impurity": | * "Entropy Impurity": | ||
| − | <math>I = \sum_{j}P(\omega _j)\log_2P(\omega _j)</math>, when priors are known, else approximate <math> P(\omega _j)</math> by | + | <math>I = \sum_{j}P(\omega _j)\log_2P(\omega _j)</math>, when priors are known, else approximate <math>P(\omega _j)</math> by |
<math>P(\omega _j) = \frac{\# of training patterns in \omega _j}{Total \# of training patterns}</math> | <math>P(\omega _j) = \frac{\# of training patterns in \omega _j}{Total \# of training patterns}</math> | ||
* "Gini Impurity:" | * "Gini Impurity:" | ||
| − | <math> I = \sum_{i\ne j}P(\omega _i)P(\omega _j) = \frac{1}{2}[1- \sum_{j}P^2(\omega _j) | + | <math>I = \sum_{i\ne j}P(\omega _i)P(\omega _j) = \frac{1}{2}[1- \sum_{j}P^2(\omega _j)</math> |
| − | Ex: when C = 2, <math> I = P(\omega _1)P(\omega _2) </math> | + | Ex: when C = 2, <math>I = P(\omega _1)P(\omega _2)</math> |
Revision as of 22:08, 1 April 2008
When the number of categories, c is big, decision tress are particularly good.
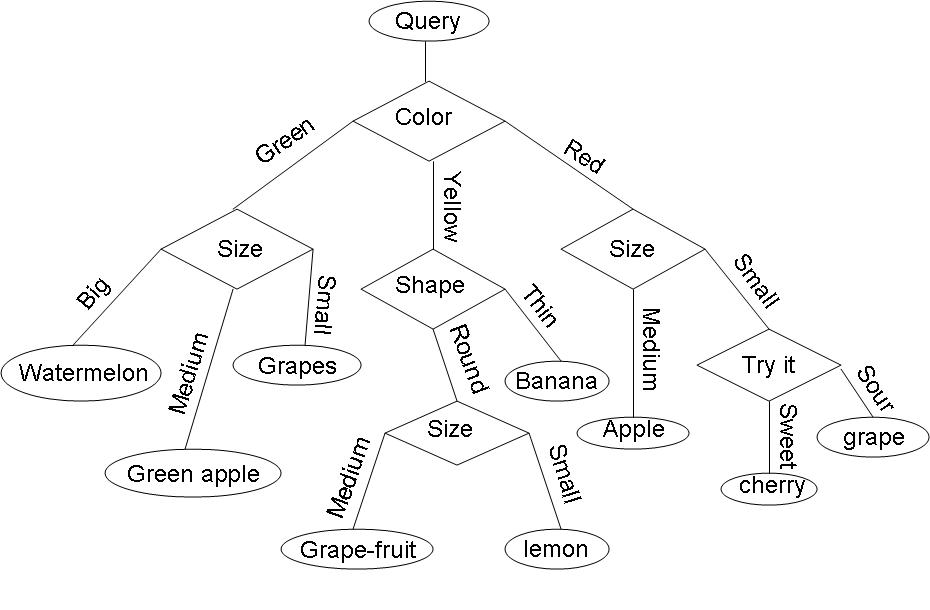
Example: Consider the query "Identify the fruit" from a set of c=7 categories {watermelon, apple, grape, lemon, grapefruit, banana, cherry} .
One possible decision tree based on simple queries is the following:
- To insert the decision tree example on fruits from class**
Three crucial questions to answer
For constructing a decision tree, for a given classification problem, we have to answer these three questions
1) Which question shoud be asked at a given node -"Query Selection"
2) When should we stop asking questions and declare the node to be a leaf -"When should we stop splitting"
3) Once a node is decided to be a leaf, what category should be assigned to this leaf -"Leaf classification"
We shall discuss questions 1 and 2 (3 being very trivial)
Need to define 'impurity' of a dataset such that $ impurity = 0 $ when all the training data belongs to one class.
Impurity is large when the training data contain equal percentages of each class
$ P(\omega _i) = \frac{1}{C} $; for all $ i $
Let $ I $ denote the impurity. Impurity can be defined in the following ways:
- "Entropy Impurity":
$ I = \sum_{j}P(\omega _j)\log_2P(\omega _j) $, when priors are known, else approximate $ P(\omega _j) $ by $ P(\omega _j) = \frac{\# of training patterns in \omega _j}{Total \# of training patterns} $
- "Gini Impurity:"
$ I = \sum_{i\ne j}P(\omega _i)P(\omega _j) = \frac{1}{2}[1- \sum_{j}P^2(\omega _j) $
Ex: when C = 2, $ I = P(\omega _1)P(\omega _2) $