Difference between revisions of "Decision Trees OldKiwi" - Rhea

Revision as of 10:24, 31 March 2008

Decision Trees

Decision trees are powerful and popular tools for classification and prediction. The attractiveness of decision trees is due to the fact that, in contrast to neural networks, decision trees represent rules. Rules can readily be expressed so that humans can understand them or even directly used in a database access language like SQL so that records falling into a particular category may be retrieved.

In some applications, the accuracy of a classification or prediction is the only thing that matters. In such situations we do not necessarily care how or why the model works. In other situations, the ability to explain the reason for a decision, is crucial. In marketing one has describe the customer segments to marketing professionals, so that they can utilize this knowledge in launching a successful marketing campaign. This domain experts must recognize and approve this discovered knowledge, and for this we need good descriptions. There are a variety of algorithms for building decision trees that share the desirable quality of interpretability.

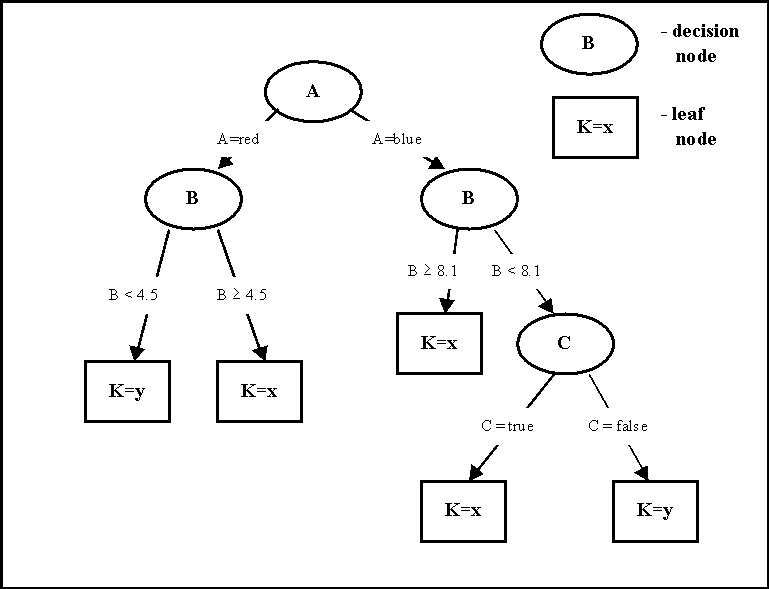
What is a Decision Tree

Decision tree is a classifier in the form of a tree structure (see figure below), where each node is either:

• a leaf node - indicates the value of the target attribute (class) of examples, or
• a decision node - specifies some test to be carried out on a single attribute-value, with one branch and sub-tree for each possible outcome of the test.

A decision tree can be used to classify an example by starting at the root of the tree and moving through it until a leaf node, which provides the classification of the instance.

Decision tree induction is a typical inductive approach to learn knowledge on classification. The key requirements to do mining with decision trees are:

• Attribute-value description: object or case must be expressible in terms of a fixed collection of properties or attributes. This means that we need to discretize continuous attributes, or this must have been provided in the algorithm.
• Predefined classes (target attribute values): The categories to which examples are to be assigned must have been established beforehand (supervised data).
• Discrete classes: A case does or does not belong to a particular class, and there must be more cases than classes.
• Sufficient data: Usually hundreds or even thousands of training cases.

Constructing a Decision Tree

Most algorithms that have been developed for learning decision trees are variations on a core algorithm that employs a top-down, greedy search through the space of possible decision trees. Decision tree programs construct a decision tree T from a set of training cases.

J. Ross Quinlan originally developed ID3 at the University of Sydney. He first presented ID3 in 1975 in a book, Machine Learning, vol. 1, no. 1. ID3 is based on the Concept Learning System (CLS) algorithm.

Decision Tree Algorithm:

function ID3
Input:   (R: a set of non-target attributes, C: the target attribute, S: a training set) returns a decision tree;
 begin
  If S is empty, return a single node with 
     value Failure;
  If S consists of records all with the same 
     value for the target attribute, 
     return a single leaf node with that value;
  If R is empty, then return a single node 
     with the value of the most frequent of the
     values of the target attribute that are 
     found in records of S; [in that case 
     there may be be errors, examples 
     that will be improperly classified];
  Let A be the attribute with largest 
     Gain(A,S) among attributes in R;
  Let {aj| j=1,2, .., m} be the values of 
     attribute A;
  Let {Sj| j=1,2, .., m} be the subsets of 
     S consisting respectively of records 
     with value aj for A;
  Return a tree with root labeled A and arcs 
     labeled a1, a2, .., am going respectively 
     to the trees (ID3(R-{A}, C, S1), ID3(R-{A}, C, S2),
     .....,ID3(R-{A}, C, Sm);
  Recursively apply ID3 to subsets {Sj| j=1,2, .., m}
     until they are empty
 end

Best Classifiers

The estimation criterion in the decision tree algorithm is the selection of an attribute to test at each decision node in the tree. The goal is to select the attribute that is most useful for classifying examples. A good quantitative measure of the worth of an attribute is a statistical property called information gain that measures how well a given attribute separates the training examples according to their target classification. This measure is used to select among the candidate attributes at each step while growing the tree.

Problems with Decision Trees

Practical issues in learning decision trees include determining how deeply to grow the decision tree, handling continuous attributes, choosing an appropriate attribute selection measure, handling training data with missing attribute values, handing attributes with differing costs, and improving computational efficiency. Below we discuss each of these issues and extensions to the basic ID3 algorithm that address them.

Avoiding Over-Fitting

In principle decision tree algorithm described previously can grow each branch of the tree just deeply enough to perfectly classify the training examples. While this is sometimes a reasonable strategy, in fact it can lead to difficulties when there is noise in the data, or when the number of training examples is too small to produce a representative sample of the true target function. In either of these cases, this simple algorithm can produce trees that over-fit the training examples.

Over-fitting is a significant practical difficulty for decision tree learning and many other learning methods. There are several approaches to avoiding over-fitting in decision tree learning. These can be grouped into two classes:

• approaches that stop growing the tree earlier, before it reaches the point where it perfectly classifies the training data,
• approaches that allow the tree to over-fit the data, and then post prune the tree.

Although the first of these approaches might seem more direct, the second approach of post-pruning over-fit trees has been found to be more successful in practice. This is due to the difficulty in the first approach of estimating precisely when to stop growing the tree.

Regardless of whether the correct tree size is found by stopping early or by post-pruning, a key question is what criterion is to be used to determine the correct final tree size. Approaches include:

• Use a separate set of examples, distinct from the training examples, to evaluate the utility of post-pruning nodes from the tree.
• Use all the available data for training, but apply a statistical test to estimate whether expanding (or pruning) a particular node is likely to produce an improvement beyond the training set.
• Use an explicit measure of the complexity for encoding the training examples and the decision tree, halting growth of the tree when this encoding size is minimized. This approach is based on a heuristic called the Minimum Description Length principle.

The first of the above approaches is the most common and is often referred to as a training and validation set approach. In this approach, the available data are separated into two sets of examples: a training set, which is used to form the learned hypothesis, and a separate validation set, which is used to evaluate the accuracy of this hypothesis over subsequent data and, in particular, to evaluate the impact of pruning this hypothesis.

Strengths and Weakness of Decision Trees

Strengths:

• Decision trees are able to generate understandable rules.
• Decision trees perform classification without requiring much computation.
• Decision trees are able to handle both continuous and categorical variables.
• Decision trees provide a clear indication of which fields are most important for prediction or classification.

Weaknesses:

• Decision trees are less appropriate for estimation tasks where the goal is to predict the value of a continuous attribute.
• Decision trees are prone to errors in classification problems with many class and relatively small number of training examples.
• Decision tree can be computationally expensive to train. The process of growing a decision tree is computationally expensive. At each node, each candidate splitting field must be sorted before its best split can be found. In some algorithms, combinations of fields are used and a search must be made for optimal combining weights. Pruning algorithms can also be expensive since many candidate sub-trees must be formed and compared.
• Decision trees do not treat well non-rectangular regions. Most decision-tree algorithms only examine a single field at a time. This leads to rectangular classification boxes that may not correspond well with the actual distribution of records in the decision space.

References

Information collected from [1]

Other tutorials on Decision Trees:

• [2]
• [3]
• [4]