m |
|||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
This section gives a brief outline about probabilistic neural networks (PNN) and General Regression Neural Networks (GRNN). Although these two are similar in architectures, they disagree in philosophy in that, PNNs? perform a classification when the target variable is categorical, whereas GRNNs? perform a classification on continuous target vatiables. | This section gives a brief outline about probabilistic neural networks (PNN) and General Regression Neural Networks (GRNN). Although these two are similar in architectures, they disagree in philosophy in that, PNNs? perform a classification when the target variable is categorical, whereas GRNNs? perform a classification on continuous target vatiables. | ||
| Line 14: | Line 12: | ||
[[Image:second_OldKiwi.jpg]] | [[Image:second_OldKiwi.jpg]] | ||
| + | |||
| + | [[Category:ECE662]] | ||
Latest revision as of 07:47, 10 April 2008
This section gives a brief outline about probabilistic neural networks (PNN) and General Regression Neural Networks (GRNN). Although these two are similar in architectures, they disagree in philosophy in that, PNNs? perform a classification when the target variable is categorical, whereas GRNNs? perform a classification on continuous target vatiables.
PNNs work on a very similar principal as that of K-Nearest Neighbor (k-NN) models. The idea is that, a a predicted target value of an item is likely to be about the same as other items that have close values of the predictor variables.
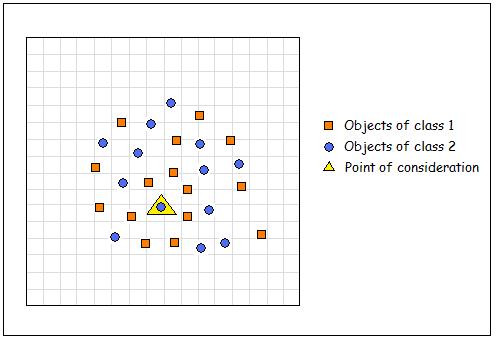
Consider the figure shown above. The orange symbols represent class 1 and the blue ones represent class 2. Now the yellow symbol represents the case that we are trying to classify. On observing the location of that particular symbol, it is surrounded by the orange symbols. Now, when we use the distance from the mean as a criterion, this classification is bound to go wrong, in spite of the fact that the yellow symbol exactly rests on the blue one. this ambiguity is attributed to the fact the placement of this particular blue symbol is rather unusual.
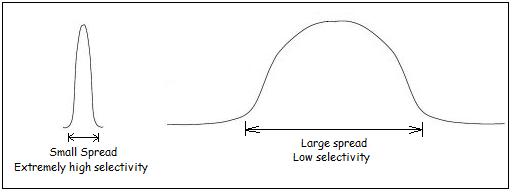
The PNN considers the effects of all points surrounding the given point in arriving at a decision. The distance is computed from the point being evaluated to each of the other points, and a radial basis function (RBF) (also called a kernel function) is applied to the distance to compute the weight (influence) for each point. The radial basis function is so named because the radius distance is the argument to the function.
The weight is calculated as a function of its radial distance. i.e, the farther the point is, the lesser influence it exhibits on a particular point. The gaussian function is a commonly used RBF.