| Line 13: | Line 13: | ||
Example | Example | ||
[[Image:hypersurface_example_OldKiwi.jpg]] | [[Image:hypersurface_example_OldKiwi.jpg]] | ||
| + | |||
Clarification 2 - All classifiers are defined by hypersurfaces. - Consider a Nearest Neighbor classification problem: The classification of any query is decided by the label of its nearest neighbor. It may not be clear how this classifier can be defined by hypersurface. But we can define separating hypersurfaces which pass mid-way between points of different classes. In the extreme case, there can be a hypersurface for each data point enveloping all queries that will be classified with the label of that data point. | Clarification 2 - All classifiers are defined by hypersurfaces. - Consider a Nearest Neighbor classification problem: The classification of any query is decided by the label of its nearest neighbor. It may not be clear how this classifier can be defined by hypersurface. But we can define separating hypersurfaces which pass mid-way between points of different classes. In the extreme case, there can be a hypersurface for each data point enveloping all queries that will be classified with the label of that data point. | ||
Revision as of 00:01, 10 March 2008
LECTURE THEME :
Bayes classification
Topics:
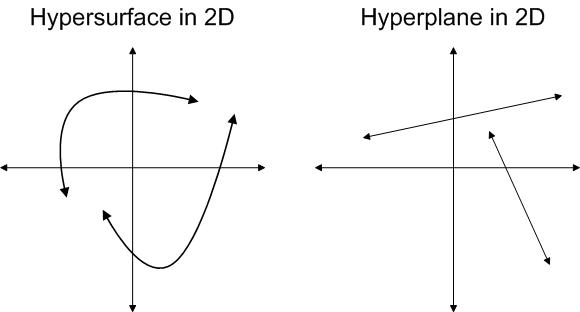
Clarification 1 - Difference between Hyperplane and Hypersurface: In simple terms, a hypersurface is any n-1 dimensional surface in n-dimensional space, while hyperplane is a flat hypersurface.
Clarification 2 - All classifiers are defined by hypersurfaces. - Consider a Nearest Neighbor classification problem: The classification of any query is decided by the label of its nearest neighbor. It may not be clear how this classifier can be defined by hypersurface. But we can define separating hypersurfaces which pass mid-way between points of different classes. In the extreme case, there can be a hypersurface for each data point enveloping all queries that will be classified with the label of that data point.